Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.45|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.46|11 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.43|20 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.44
- An ammeter A of finite resistance, and a resistor R are joined in seri...
Text Solution
|
- The capacitor 'C' is initially unchanged. Switch S(1) is closed for a ...
Text Solution
|
- In the figure shown below, the maximum and the minimum possible unknow...
Text Solution
|
- In front of an earthed conductor a point charge +q is placed a shown i...
Text Solution
|
- Two potentiometer wires w(1) and w(2) of equal length l connected to a...
Text Solution
|
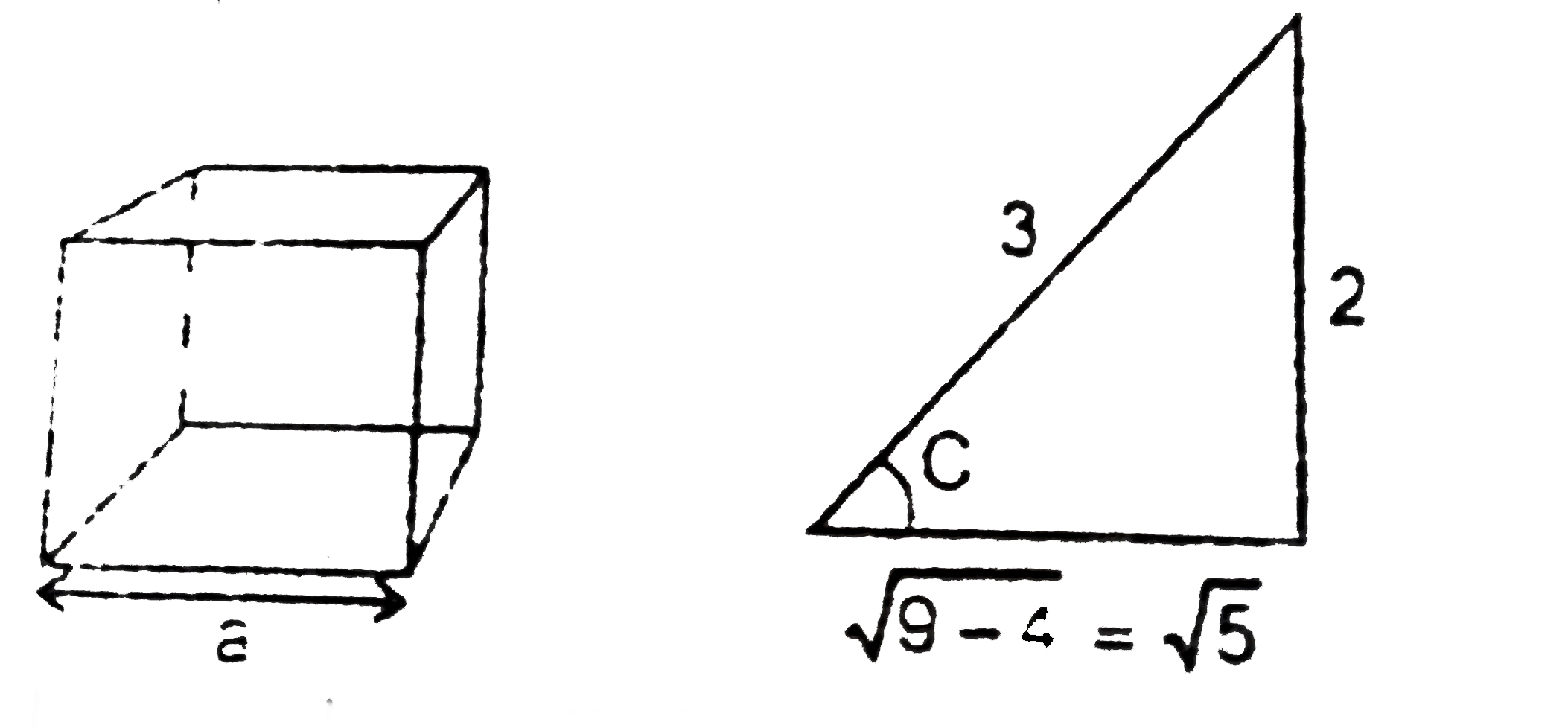
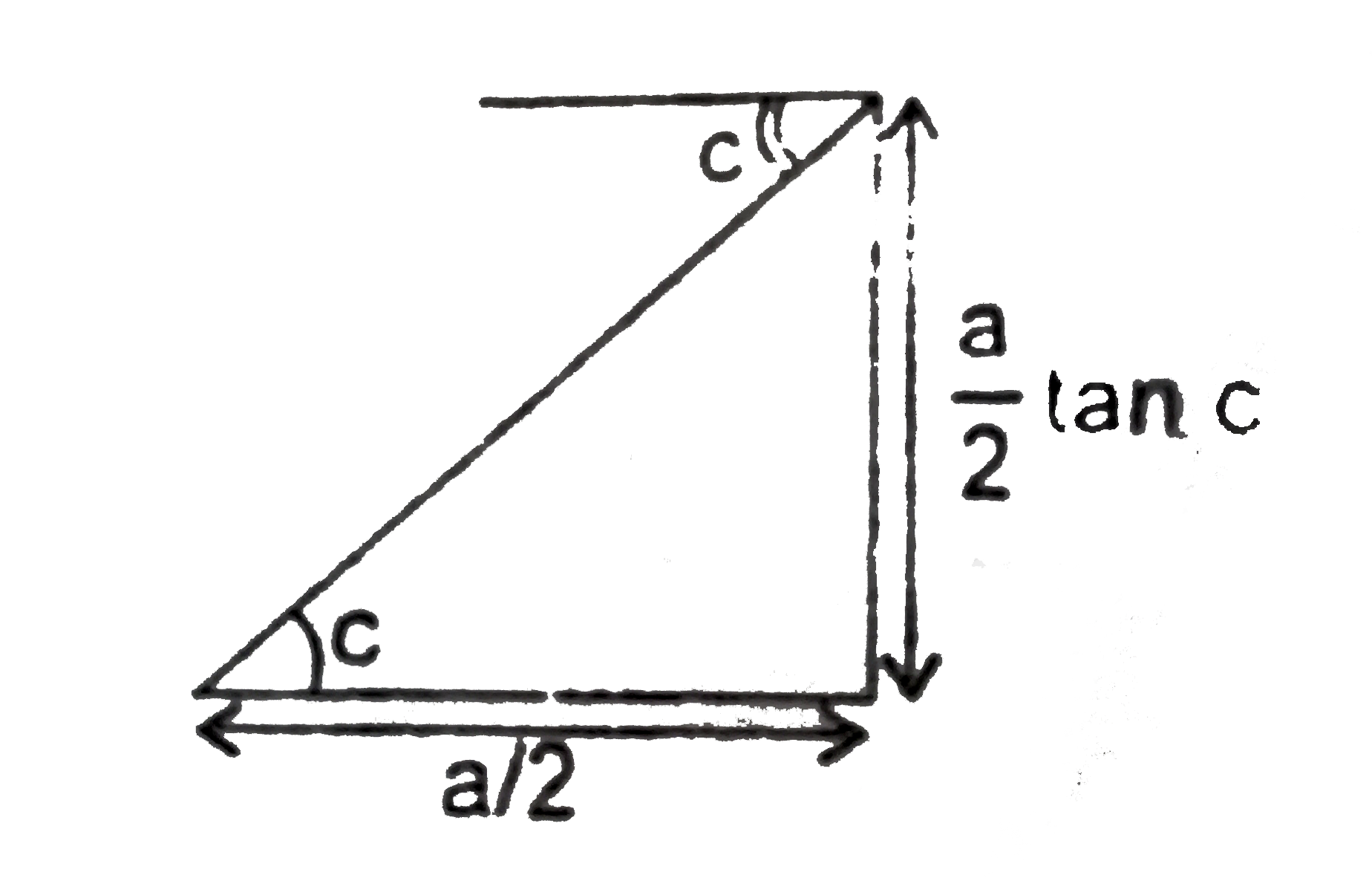
- A transparent solid cube of side 'a' has refractive index 3/2. A point...
Text Solution
|
- An experimental setup of verification of photoelectric effect is shown...
Text Solution
|
- An experimental setup of verification of photoelectric effect is shown...
Text Solution
|
- An experimental setup of verification of photoelectric effect is shown...
Text Solution
|
- An experimental setup of verification of photoelectric effect is shown...
Text Solution
|