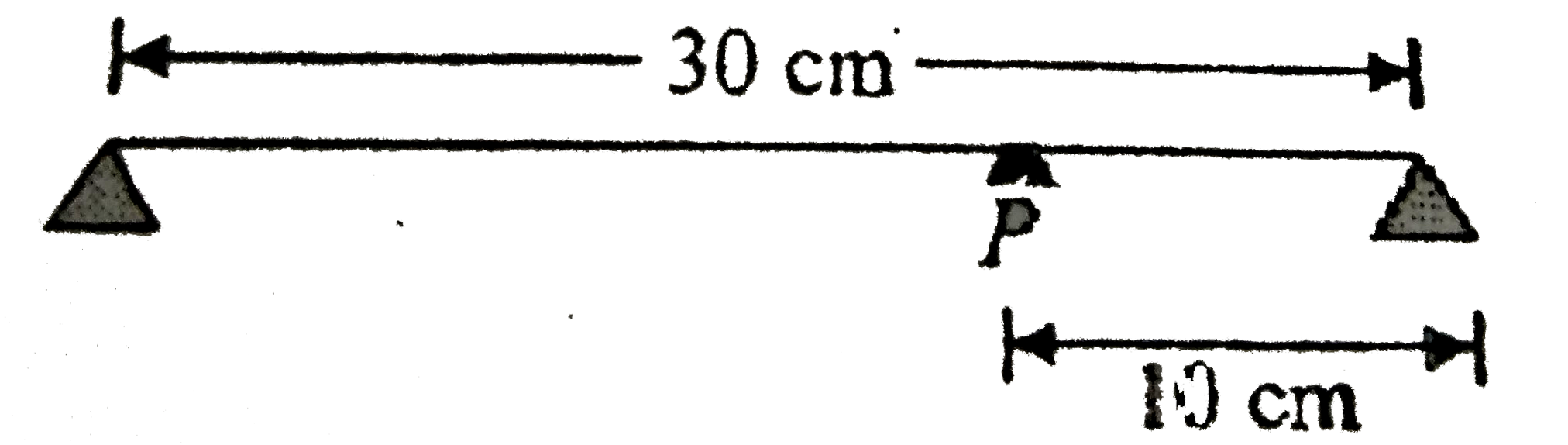A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.69|20 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.70|9 VideosDAILY PRACTICE PROBLEM
RESONANCE|Exercise DPP No.67|10 VideosCURRENT ELECTRICITY
RESONANCE|Exercise High Level Problems (HIP)|21 VideosELECTRO MAGNETIC WAVES
RESONANCE|Exercise Exercise 3|27 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEM-DPP No.68
- Three particles each of mass m can slide on fixed frictionless horizon...
Text Solution
|
- A particular hydrogen like atom has its ground state Binding energy = ...
Text Solution
|
- The capacitance of a parallel plate capacitor is C when the region bet...
Text Solution
|
- In a balanced wheat stone bridge, current in the galvanometer is zero....
Text Solution
|
- A plank of mass 4m is placed on a smooth horizontal surface and a spri...
Text Solution
|
- Two steel ball of equal diameter are connected by a rigid bar of negli...
Text Solution
|
- Figure shown a clamped metal string of length 30 cm and linear mass de...
Text Solution
|
- Figure shown a clamped metal string of length 30 cm and linear mass de...
Text Solution
|
- Figure shown a clamped metal string of length 30 cm and linear mass de...
Text Solution
|