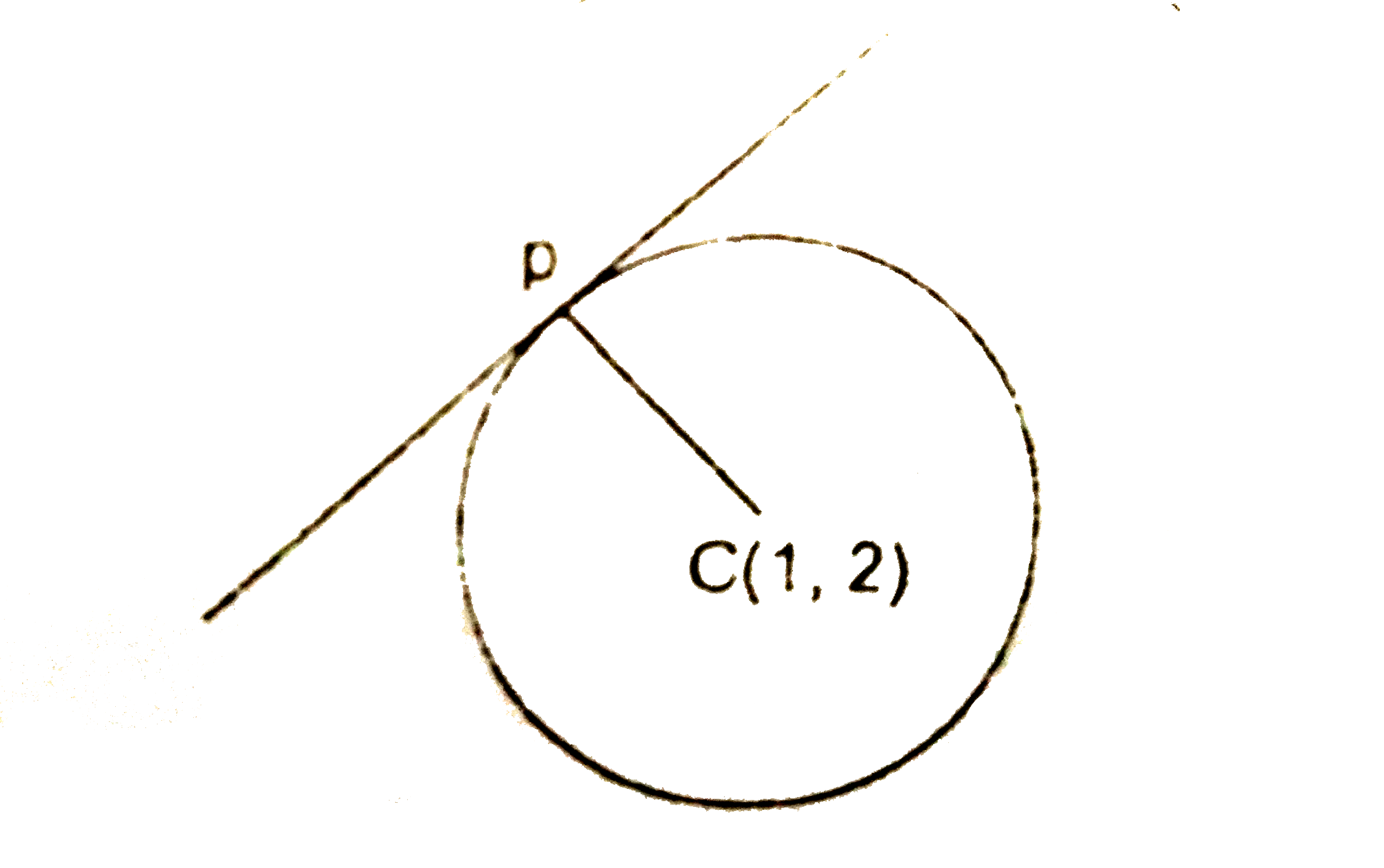A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RESONANCE-TEST PAPERS-MATHEMATICS
- If x(1),x(2)……..x(n) be n observation and barx be their arithmeti...
Text Solution
|
- The negation of the compound proposition p vv ( ~ p vv q) is
Text Solution
|
- A line L is perpendicular to the line 3x-4y-7=0 and touches the circle...
Text Solution
|
- The value of cos^(-1)(cos(2tan^(-1)((sqrt(3)+1)/(sqrt(4-2sqrt(3))))))...
Text Solution
|
- If P(B)=3/4, P(AnnBnnbarC)=1/3 and P(barAnnBbarC)=1/3 then P(BnnC)=
Text Solution
|
- sum(r=1)^(n) 1/(log(2^(r))4) is equal to
Text Solution
|
- In how many types ways can five different examination papers of maths...
Text Solution
|
- The area covered by the curve y=max{2-x,2,1+x} with x-axis from x=-1 t...
Text Solution
|
- If f(x)=x^(3)+3x^(2)+4x+asinx+bcosx, forall x in R is a one-one fuctio...
Text Solution
|
- Given the relation R={(1,2),(2,3) on the set A={1,2,3}, add a minimum ...
Text Solution
|
- If 2a x-2y+3z=0,x+a y+2z=0,a n d2+a z=0 have a nontrivial solution,...
Text Solution
|
- The number of value(s) of x satisfying 1-log9(x+1)^2=1/2log(sqrt(3))((...
Text Solution
|
- Total number of ordered pairs (x, y) satisfying Iyl = cos x and y = si...
Text Solution
|
- If f(x+y)=2f(x) f(y) for all x,y where f'(0)=3 and f'(4)=2, then f'(4)...
Text Solution
|
- If A is a square matrix such that A(adjA)=[(4,0,0),(0,4,0),(0,0,4)], t...
Text Solution
|
- Let f(x) be a function whose domain is [-5, 7] and g(x) = |2x + 5|, th...
Text Solution
|
- f(x)=x^x , x in (0,oo) and let g(x) be inverse of f(x) , then g(x)'...
Text Solution
|
- Suppose that f is an even, periodic function with period 2,a n dt h a ...
Text Solution
|
- The value of sin^(-1){cot(sin^(-1)(sqrt((2-sqrt3)/4)+cos^(-1)(sqrt(12)...
Text Solution
|
- The number of real solutions of cos^-1 x + cos^-1 2 x = -pi is
Text Solution
|