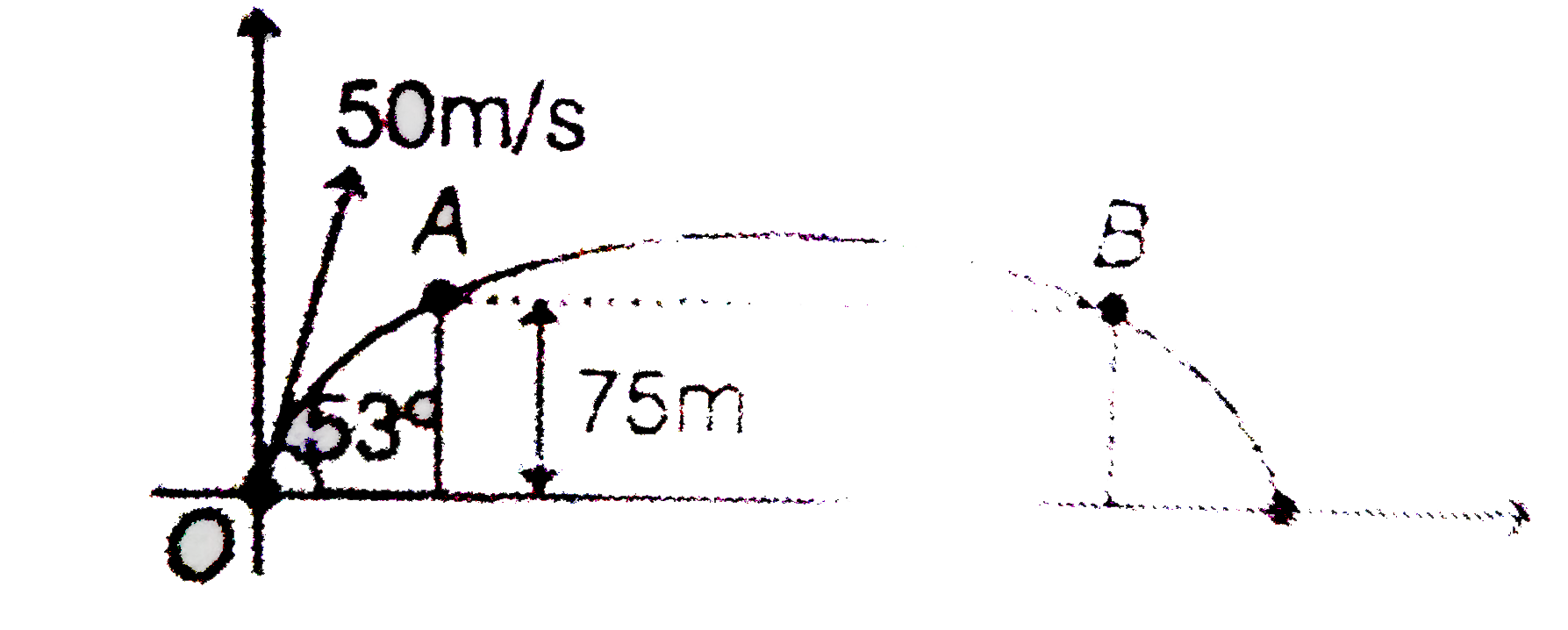A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-KINEMATICS-COMPREHENSION_TYPE
- Velocity of a projectile at height 15 m from ground is v=(20hati+10hat...
Text Solution
|
- Velocity of a projectile at height 15 m from ground is v=(20hati+10hat...
Text Solution
|
- Velocity of a projectile at height 15 m from ground is v=(20hati+10hat...
Text Solution
|
- Velocity of a projectile at height 15 m from ground is v=(20hati+10hat...
Text Solution
|
- At t=0 a projectile is fired from a point O (taken as origin) on the g...
Text Solution
|
- At t=0 a projectile is fired from a point O (taken as origin) on the g...
Text Solution
|
- There of the fundamental constant of physics are the universal gravit...
Text Solution
|
- There of the fundamental constant of physics are the universal gravit...
Text Solution
|
- There of the fundamental constant of physics are the universal gravit...
Text Solution
|
- Two friends A and b playing a game of collision of balls and throwing ...
Text Solution
|
- Two friends A and b playing a game of collisionn of balls and throwing...
Text Solution
|
- A particle of mass m is projected up from the bottom of an inclined pl...
Text Solution
|
- A particle of mass m is projected up from the bottom of an inclined pl...
Text Solution
|