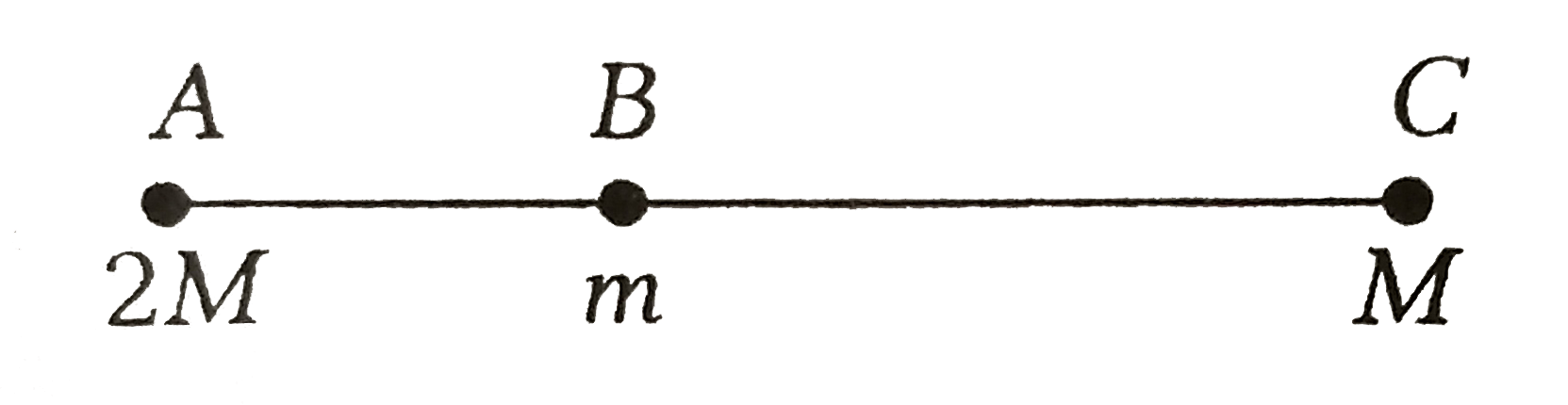A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-GRAVITATION-(A) Chapter Exercises
- Two satellite of same mass are launched in the same orbit of radius r ...
Text Solution
|
- Compute the additional velocity required by a satellite orbiting aroun...
Text Solution
|
- Particles of masses 2M, m and M are respectively at points A, B and C ...
Text Solution
|
- Earth orbiting satellite will escape if
Text Solution
|
- Energy required in moving a body of mass m from a distance 2R to 3R fr...
Text Solution
|
- A body attains a height equal to the radius of the earth. The velocity...
Text Solution
|
- Suppose the gravitational attraction varies inversely as the distance ...
Text Solution
|
- The rotation of the earth about its axis speeds up such that a man on ...
Text Solution
|
- The rotation of the earth radius R about its axis speeds upto a value ...
Text Solution
|
- Assuming the radius of the earth to be 6.5 xx 10^(6) m. What is the ti...
Text Solution
|
- If gravitational attraction between two points masses be given by F=G(...
Text Solution
|
- Suppose the gravitational force varies inversely as the n^(th) power o...
Text Solution
|
- A body is projected vertically upwards from the surface of the earth w...
Text Solution
|
- A particle takes a time t(1) to move down a straight tunnel from the s...
Text Solution
|
- An earth satellite of mass m revolves in a circular orbit at a height ...
Text Solution
|
- A body which is initially at rest at a height R above the surface of t...
Text Solution
|
- A planet of mass m moves around the Sun of mass Min an elliptical orbi...
Text Solution
|
- A rocket is launched vertical from the surface of the earth of radius ...
Text Solution
|
- Two particles of equal mass (m) each move in a circle of radius (r) un...
Text Solution
|
- Suppose a smooth tunnel is dug along a straight line joining two point...
Text Solution
|