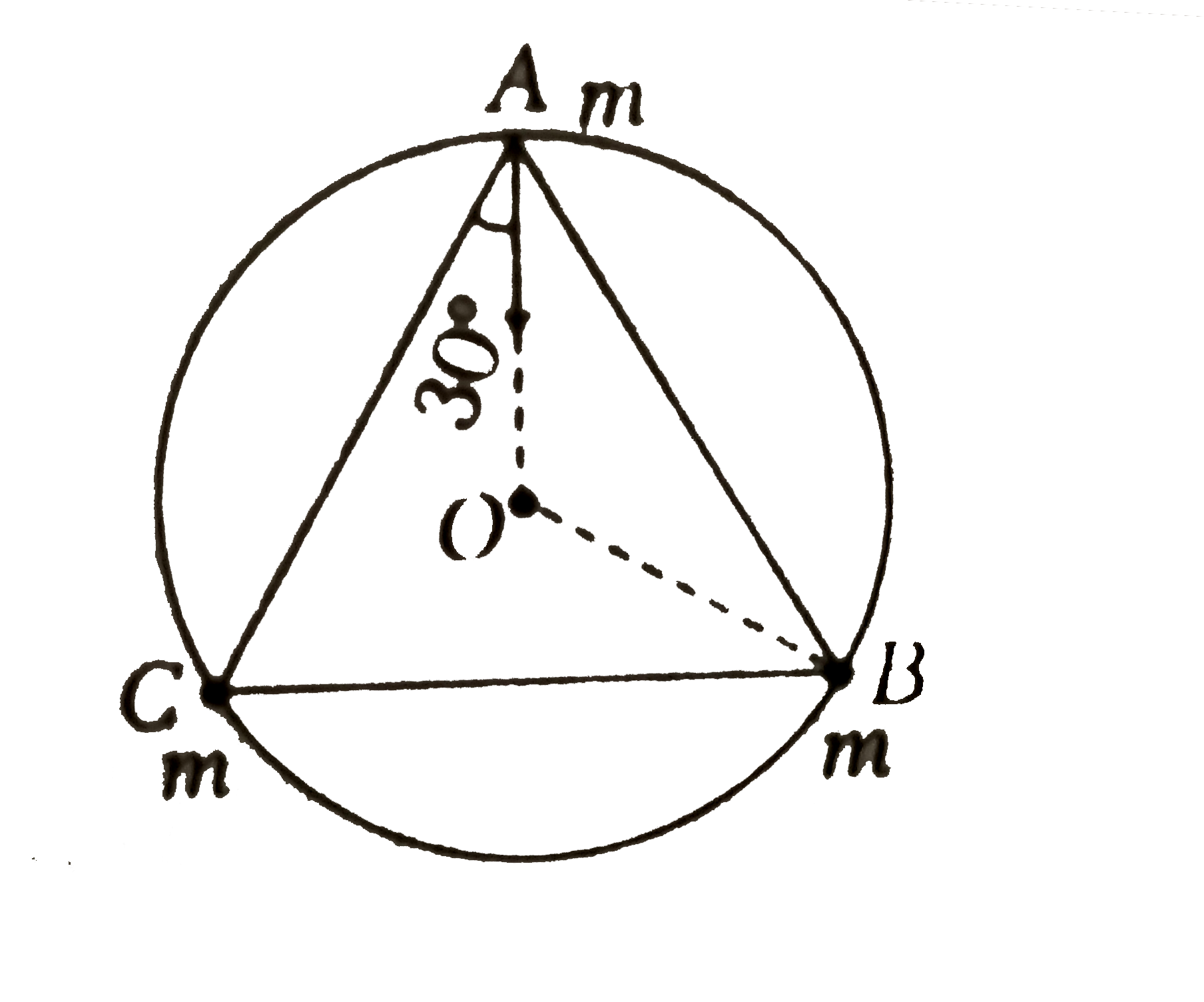
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-GRAVITATION-(A) Chapter Exercises
- Four equal masses (each of mass M) are placed at the corners of a squa...
Text Solution
|
- Energy of a satellite in circular orbit is E(0). The energy required t...
Text Solution
|
- Pertaining to two planets, the ratio of escape velocities from respect...
Text Solution
|
- An object is released from a height twice the radius of the earth on t...
Text Solution
|
- A planet of mass m revolves in elliptical orbit around the sun of mass...
Text Solution
|
- The magnitude of the gravitational field at distance r(1) and r(2) fro...
Text Solution
|
- Two particles of mass m and M are initialljy at rest at infinite dista...
Text Solution
|
- The ratio of energy required to raise a satellite to a height h above ...
Text Solution
|
- A small body of superdense material, whose mass is twice the mass of t...
Text Solution
|
- Let E be the energy required to raise a satellite to height h above ea...
Text Solution
|
- A satellite is revolving round the earth with orbital speed v(0) if it...
Text Solution
|
- Four particles, each of mass M and equidistant from each other, move a...
Text Solution
|
- Three particle each of mass m, are located at the vertices of an equil...
Text Solution
|
- Three point masses each of mass m rotate in a circle of radius r with ...
Text Solution
|
- Two identical thin rings each of radius R are coaxially placed at a di...
Text Solution
|
- A solid sphere of mass M and radius R has a spherical cavity of radius...
Text Solution
|
- A point P(R sqrt(3),0,0) lies on the axis of a ring of mass M and radi...
Text Solution
|
- A mass m is at a distance a from one end of a uniform rod of length l ...
Text Solution
|
- A solid sphere of uniform density and radius R applies a gravitational...
Text Solution
|
- Suppose a vertical tunnel is dug along the diameter of earth , which i...
Text Solution
|