A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
BITSAT GUIDE-GRAVITATION-BITSAT Archives
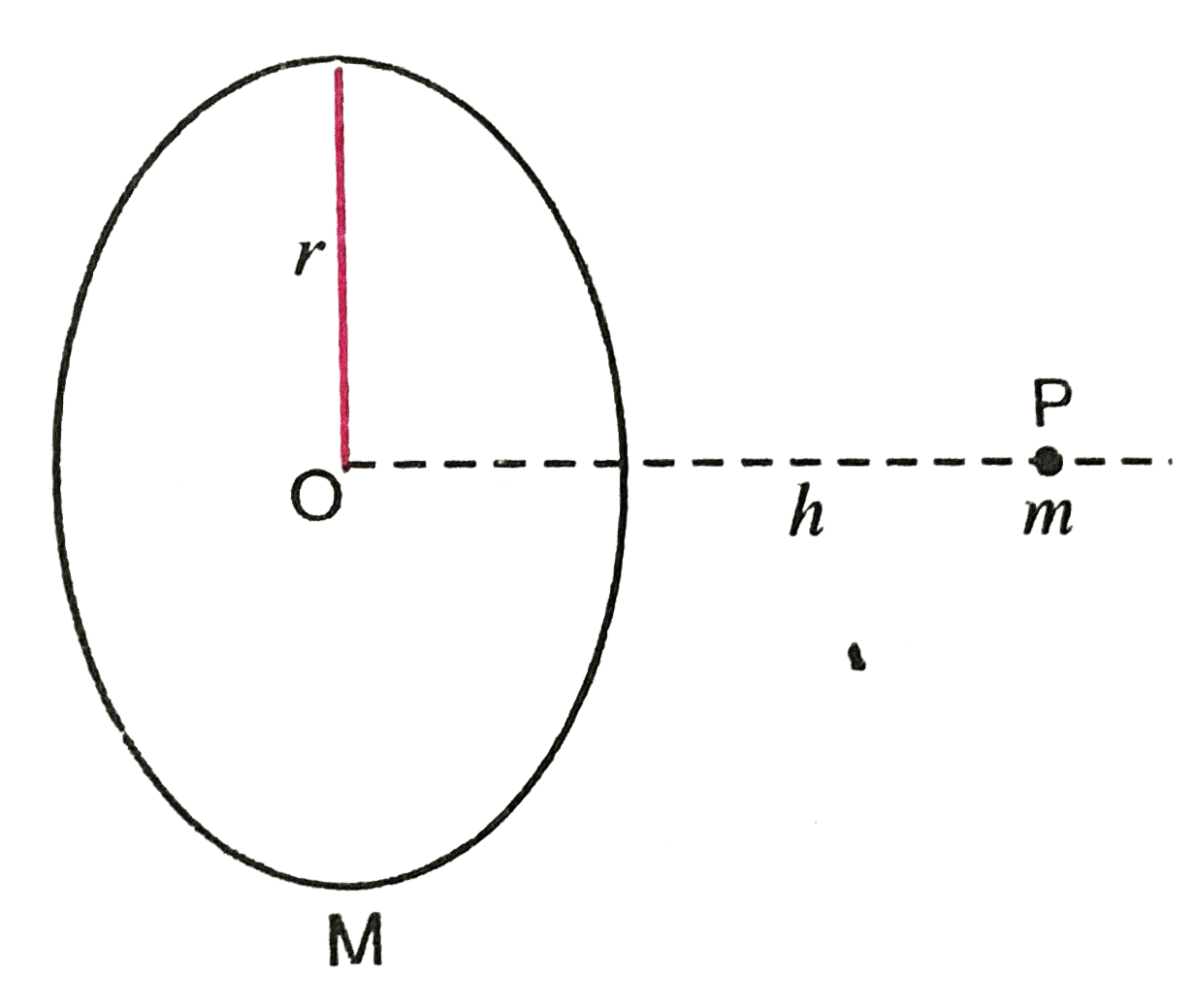
- A mass m is placed at P a distance h along the normal through the cent...
Text Solution
|
- The total energy of a revolving satellite around the earth is -KJ. The...
Text Solution
|
- There is a shell of mass M and density of shell is uniform. The work d...
Text Solution
|
- A satellite is in a circular orbit round the earth at an altitude R a...
Text Solution
|
- Which is constant, the earth revolving around the sun ?
Text Solution
|
- Suppose the gravitational force varies inversely as the nth power of d...
Text Solution
|
- The satellite of mass m revolving in a circular orbit of radius r arou...
Text Solution
|
- If a new planet is discovered rotating around Sun with the orbital rad...
Text Solution
|
- If the radius of the earth were to shrink by 1% its mass remaining the...
Text Solution
|
- The mean radius of the earth's orbit around the sun is 1.5 xx 10^(11)m...
Text Solution
|
- A satellite of mass m is orbiting around the earth at a height equal t...
Text Solution
|
- A small mass m is moved slowly from the surface of the earth to a heig...
Text Solution
|
- The orbit of geostationary satellite is circular, the time period of s...
Text Solution
|
- There are two planets. The ratio of radius of two planets is k but rat...
Text Solution
|
- A satellite of mass m is placed at a distance r from the centre of ear...
Text Solution
|
- If M is the mass of the earth and R its radius, the ratio of the gravi...
Text Solution
|