Home
Class 12
MATHS
Using integration, find the area of the ...

Using integration, find the area of the region enclosed between the two circles `x^2+y^2=4` and `(x-2)^2+y^2=4.`

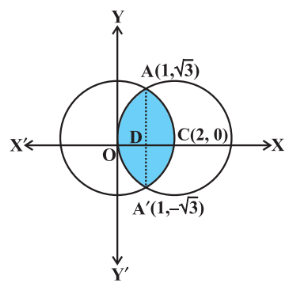
Text Solution

Verified by Experts

Equations of the given circles are `x^2+y^2=4 "(eq 1)" and (x-2)^2+y^2-4 "(eq 1)" `
Equation (1) is a circle with centre O at the origin and radius 2. Equation (2) is a circle with centre C (2, 0) and radius 2.
Solving equations (1) and (2), we have
`x=1 and y=+-sqrt3` Thus, the points of intersection of the given circles are A (1,3) and A′ (1,–3)

Required area of the enclosed region OACA′O between circles= 2 [area of the region ODCAO]
= 2 [area of the region ODAO + area of the region DCAD]
`2 [int_0^2 ydx +int_1^2 y dx]`
`2[int_0^1(sqrt(4-(x-2)^2)dx +int_1^2 sqrt(4-x^2)dx]`
now by using formula `intsqrt(x^2-x^2)=x/2 sqrt(x^2-a^2)+a^2/2sin^-1(x/a)+C`
by solving above integration and putting the value of the limits we will get
`(-sqrt3-(2pi)/3+2 pi)+ (2 pi -sqrt3 -(2 pi)/3)`
so by solving and simplifying this we will get `(8pi)/3-2sqrt3` as a final answer
Promotional Banner

Topper's Solved these Questions

  • APPLICATION OF INTEGRALS

    NCERT|Exercise EXERCISE 8.2|7 Videos

  • APPLICATION OF INTEGRALS

    NCERT|Exercise MISCELLANEOUS EXERCISE|19 Videos

  • APPLICATION OF DERIVATIVES

    NCERT|Exercise EXERCISE 6.1|18 Videos

  • CONTINUITY AND DIFFERENTIABILITY

    NCERT|Exercise QUESTION|3 Videos

Similar Questions

Explore conceptually related problems

Using integration,find the area of the region enclosed between the circles x^(2)+y^(2)=1 and (x-1)^(2)+y^(2)=1

Find the area of the region enclosed between the two circles x^(2)+y^(2)=1 and (x-1)^(2)+y^(2)=1

Find the area of the portion enclosed between the curves y^2=4x and x^2=4y .

" The area of the region enclosed between the two circles "(x-1)^(2)+y^(2)-1" and "x^(2)+(y-1)^(2)=1" is "

Using integration, find the area of the region common to the circle x^2+y^2=16 and the parabola y^2=6x .

Using integration find the area of the region bounded by y^(2)=4ax and x=4a

Using integration, find the area of the region bounded by the curve y^(2)=9x and lines x=1 and x=4.

Find the area of the region bounded by the curves x^(2)+y^(2)=4 and (x-2)^(2)+y^(2)=4.

Using integration, find the area of the region bounded by the parabola y^(2)=4x and the line x=4 .