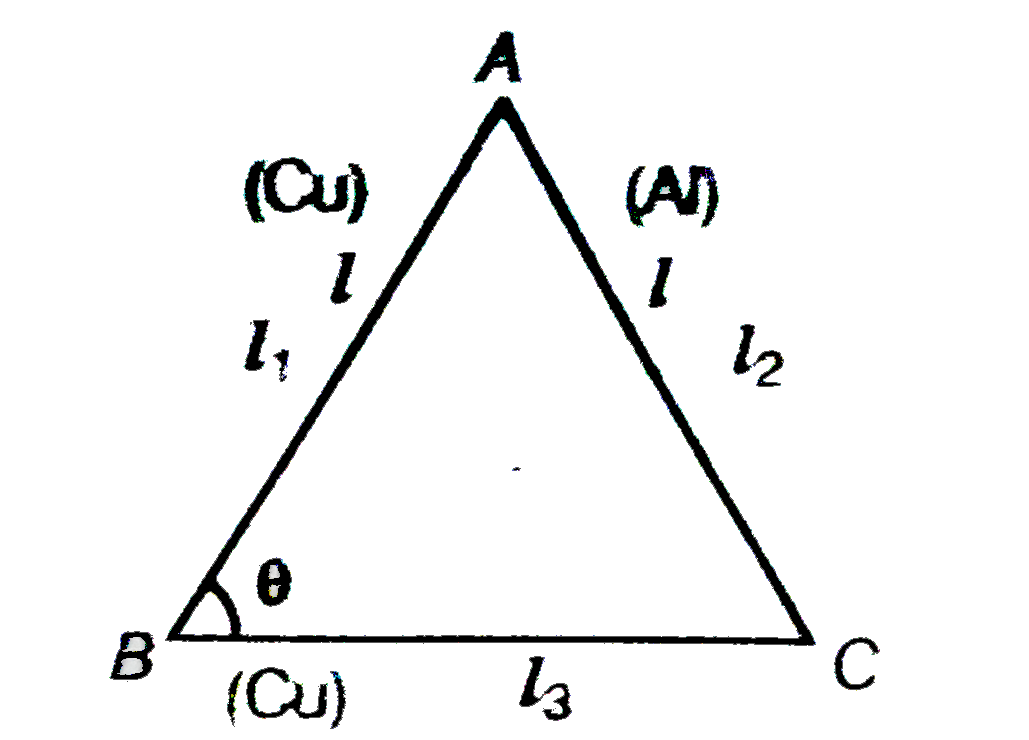Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-MECHANICAL PROPERTIES OF SOLIDS-LONG SHORT ANSWER TYPE QUESTION
- The young's modulus for steel is much more then that for rubber. For t...
Text Solution
|
- Is stress a vector quantity ?
Text Solution
|
- Two identical springs of copper and steel are equally strectched. On w...
Text Solution
|
- Young's modulus for a perfectly rigid body is
Text Solution
|
- what is the Bulk modulus for a perfect rigid body ?
Text Solution
|
- A wire of length L and radius a rigidly fixed at one end. On stretchin...
Text Solution
|
- A steel rod (Y = 2.0 xx 10^(11) N//m^(2) " and "alpha = 10^(-50).^(@)C...
Text Solution
|
- To What depth must a rubber ball be taken in deep sea so that its volu...
Text Solution
|
- A truck is pulling a car out of a ditch by means fo a steel cable that...
Text Solution
|
- Two idential solid balls, one of ivory and the other of wet caly, are...
Text Solution
|
- Consider a long steel bar under a tensile stress due to forces F, acti...
Text Solution
|
- A steel wire of mass mu per unit length with a circular cross-section ...
Text Solution
|
- A stell rod of length 2l corss sectional area A and mass M is set rot...
Text Solution
|
- An equilateral triangle ABC if formed by two Cu rods AB and BC and one...
Text Solution
|
- In nature, the failure of structural members usually result from large...
Text Solution
|
- A stone of mass m is tied to an elastic string of negligble mass and s...
Text Solution
|