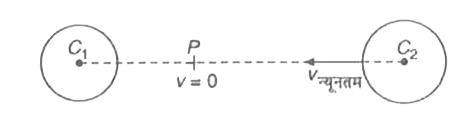लिखित उत्तर
Verified by Experts
The correct Answer is:
JEE Main & Advanced (Hindi Medium)-गुरुत्वाकर्षण -विश्लेषणात्मक प्रश्न
- दो उपग्रह S(1) व S(2) एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में...
Text Solution
|
- तीन कण, जिनमें प्रत्येक का द्रव्यमान m है, a लम्बाई भुजा वाले समबाहु त...
Text Solution
|
- एक कृत्रिम उपग्रह पृथ्वी के परित: वृत्तीय कक्षा में, पृथ्वी से पलायन व...
Text Solution
|
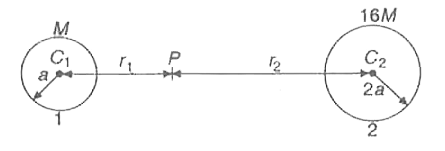
- दो नक्षत्रों के केंद्रों के बीच की दूरी 10a है। इन नक्षत्रों के द्रव्य...
Text Solution
|
- चन्द्रमा (त्रिज्या R) की सतह पर एक गड्ढा (Crater) है, जिसकी गहराई R/10...
Text Solution
|