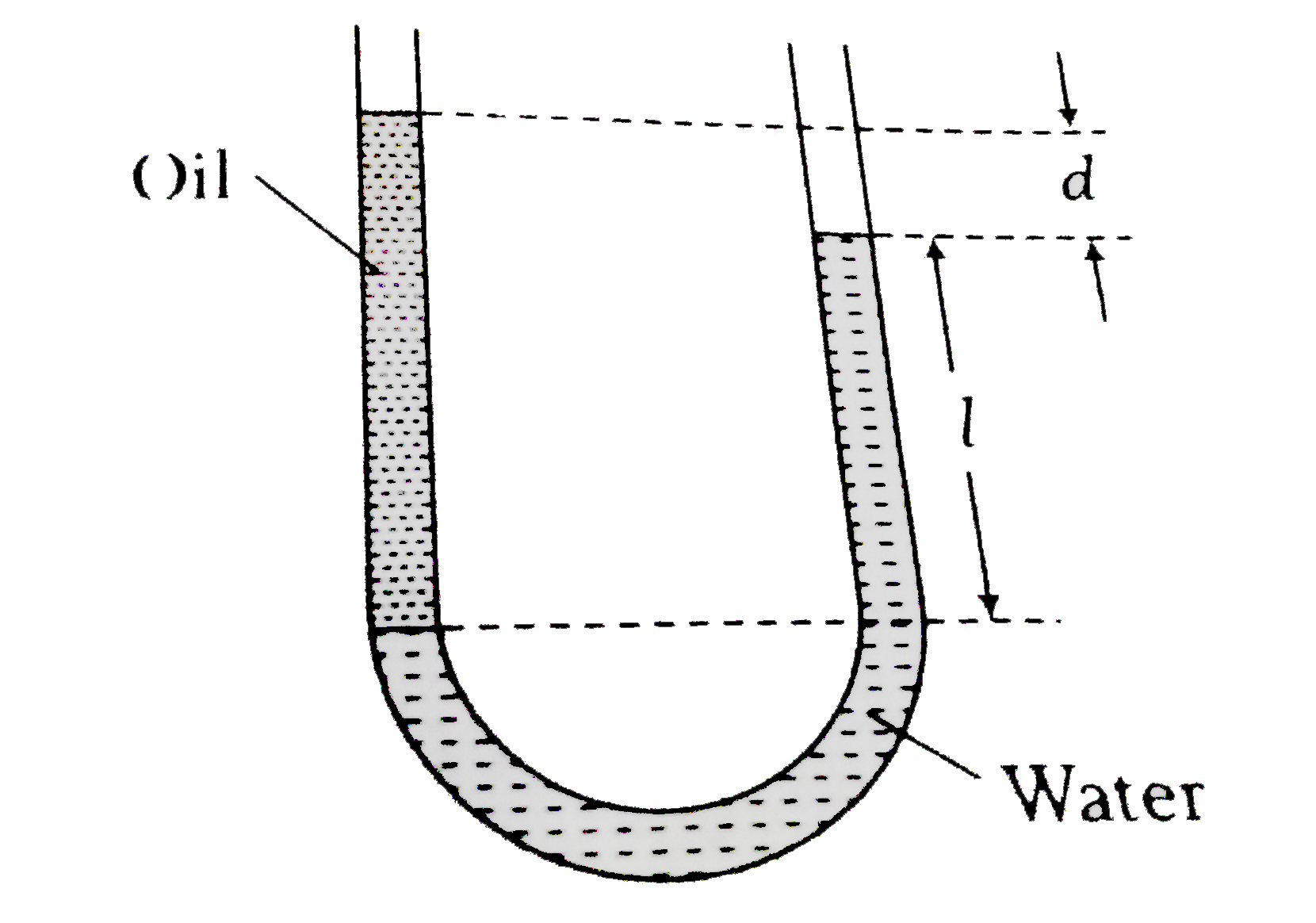A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-FLUID MECHANICS-Check point 13.1
- A fluid comparises of
Text Solution
|
- Thd dimensional formula of pressure is
Text Solution
|
- Pins and nails are made to have ponted end because
Text Solution
|
- The two thigh bones each of cross-sectional area 15 cm^(2) support the...
Text Solution
|
- Which of the following is correct.
Text Solution
|
- At a depth of 500m in an ocean (a) what is the absolute pressure? (b) ...
Text Solution
|
- Four vessels A, B, C and D have different shapes and hold different am...
Text Solution
|
- Two liquids of densities 2 rho " and " rho having their volumes in the...
Text Solution
|
- The U-tube in figure contains two different liquids in static equilibr...
Text Solution
|
- Increase in pressure at one point of the enclosed liquid in equilibriu...
Text Solution
|
- In a vehicle lifter the enclosed gas exerts a force F on a small pisto...
Text Solution
|
- What will be the length of mercury column in a barometer tube when the...
Text Solution
|
- A boat carrying a large number of stones is floating in a water tank. ...
Text Solution
|
- An iron casting containing a number of cavities weight 6000N in air an...
Text Solution
|
- A body floats in water with 40% of its volume outside water. When the ...
Text Solution
|