A
B
C
D
लिखित उत्तर
Verified by Experts
The correct Answer is:
टॉपर्स ने हल किए ये सवाल
प्रकाशिकी
JEE Main & Advanced (Hindi Medium)|Exercise बहुविकल्पीय प्रश्न - II|13 Videosप्रकाशिकी
JEE Main & Advanced (Hindi Medium)|Exercise सत्य/असत्य|6 Videosपदार्थ के गुण
JEE Main & Advanced (Hindi Medium)|Exercise शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)|2 Videosप्रयोगात्मक भौतिकी
JEE Main & Advanced (Hindi Medium)|Exercise बहुविकल्पीय प्रश्न II|3 Videos
JEE Main & Advanced (Hindi Medium)-प्रकाशिकी-श्रृंखलाबद्ध - बोधन प्रकार
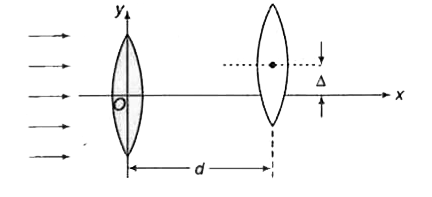
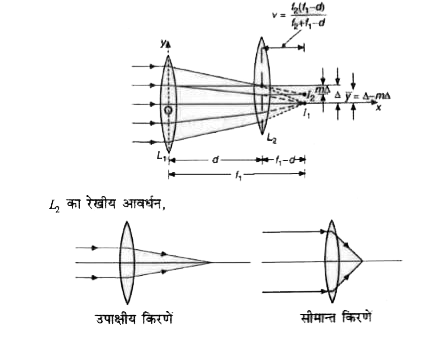
- f(1) व f(2) फोकस दूरी के दो पतले उत्तल लेंस परस्पर क्षैतिज दूरी d से...
Text Solution
|
- चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम...
Text Solution
|
- चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम...
Text Solution
|
- चित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम...
Text Solution
|
- एक प्रकाशीय तंतु में प्रकाश का परिवहन एक संरचना है जिसमें n(1) अपवर्तन...
Text Solution
|
- एक प्रकाशीय तंतु में प्रकाश का परिवहन एक संरचना है जिसमें n(1) अपवर्तन...
Text Solution
|