Text Solution
Verified by Experts
Topper's Solved these Questions
MOTION OF SYSTEM OF PARTICLES AND BODIES
PREMIERS PUBLISHERS|Exercise TEXTBOOK QUESTIONS & ANSWERS (CONCEPTUAL QUESTIONS)|16 VideosMOTION OF SYSTEM OF PARTICLES AND BODIES
PREMIERS PUBLISHERS|Exercise TEXTBOOK QUESTIONS & ANSWERS (NUMERICAL PROBLEMS)|12 VideosMOTION OF SYSTEM OF PARTICLES AND BODIES
PREMIERS PUBLISHERS|Exercise TEXTBOOK QUESTIONS & ANSWERS (SHORT ANSWER QUESTIONS)|34 VideosLAW OF MOTION
PREMIERS PUBLISHERS|Exercise OTHER IMPORTANT QUESTIONS & ANSWERS (VI Numerical Problems)|62 VideosNATURE OF PHYSICAL WORLD AND MEASUREMENT
PREMIERS PUBLISHERS|Exercise OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)|24 Videos
Similar Questions
Explore conceptually related problems
PREMIERS PUBLISHERS-MOTION OF SYSTEM OF PARTICLES AND BODIES-TEXTBOOK QUESTIONS & ANSWERS (LONG ANSWER QUESTIONS)
- Explain the types of equilibrium with suitable examples
Text Solution
|
- Explain the method to find the centre of gravity of irregularly shaped...
Text Solution
|
- Explain why a cyclist bends while negotiating a curve road?
Text Solution
|
- The moment of inertia of a Thin rod about and axis passing through the...
Text Solution
|
- Derive the expression for moment of inertia of a uniform ring about a...
Text Solution
|
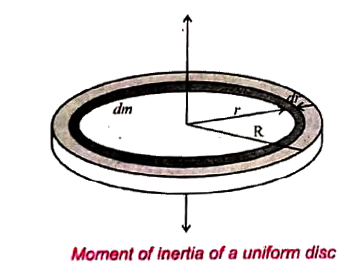
- Derive the expression for moment of inerita of a uniform disc about an...
Text Solution
|
- State conservation of angular momentum.
Text Solution
|
- State and prove parallel axis theorem
Text Solution
|
- State and prove perpendicular axis theorem.
Text Solution
|
- Discuss the effect of rolling on inclined plane and derive the express...
Text Solution
|
- Explain the types of equilibrium with suitable examples
Text Solution
|
- Explain the method to find the centre of gravity of irregularly shaped...
Text Solution
|
- Explain why a cyclist bends while negotiating a curve road?
Text Solution
|
- Derive the expresssion for moment of inertia of a rod about its centre...
Text Solution
|
- Derive the expression for moment of inertia of a uniform ring about a...
Text Solution
|
- Derive the expression for moment of inerita of a uniform disc about an...
Text Solution
|
- State conservation of angular momentum.
Text Solution
|
- State and prove parallel axis theorem
Text Solution
|
- State and prove perpendicular axis theorem.
Text Solution
|
- Discuss the effect of rolling on inclined plane and derive the express...
Text Solution
|