A
B
C
D
लिखित उत्तर
Verified by Experts
The correct Answer is:
टॉपर्स ने हल किए ये सवाल
परवलय
JEE Main & Advanced (Hindi Medium)|Exercise बहुविकल्पीय प्रश्न II|7 Videosपरवलय
JEE Main & Advanced (Hindi Medium)|Exercise रिक्त स्थानों की पूर्ति कीजिये|1 Videosनिश्चित समाकलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णाक प्रश्न|7 Videosप्रतिलोम वृत्तीय फलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णांक प्रश्न|1 Videos
JEE Main & Advanced (Hindi Medium)-परवलय-एकल पूर्णांक प्रश्न
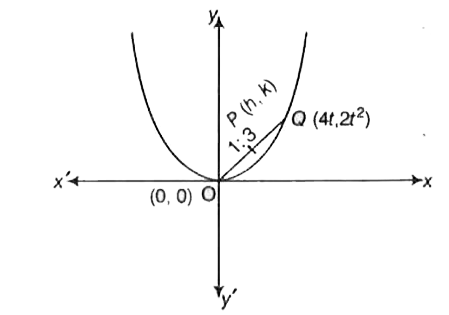
- माना O शीर्ष तथा Q परवलय: x^(2)=8y पर स्थित कोई बिन्दु है। यदि बिन्दु ...
Text Solution
|
- y^(2)=8x एक परवलय है। मान लीजिए एक त्रिभुज का क्षेत्रफल है जो नाभिलम्ब...
Text Solution
|
- परवलय y^(2)=8x की नाभि S है और PQ इस परवलय और वृत्त x^(2)+y^(2)-2x-4y=...
Text Solution
|
- माना कि वक्र C, रेखा x+y+4=0 के सापेक्ष में, परवलय (parabola) y^2=4x...
Text Solution
|
- यदि परवलय (parabola) y^(2)=4x के नाभिलम्ब जीवा (latusrectum) के शिखर ब...
Text Solution
|
- माना दीर्घवृत्त x^(2)/9+y^(2)/5=1 की नाभियाँ (foci) (f(1),0)" और "(f(2...
Text Solution
|