A
B
C
D
लिखित उत्तर
Verified by Experts
The correct Answer is:
टॉपर्स ने हल किए ये सवाल
परवलय
JEE Main & Advanced (Hindi Medium)|Exercise मैट्रिक्स-सुमेल प्रकार|2 Videosपरवलय
JEE Main & Advanced (Hindi Medium)|Exercise दृढ़कथन-कारण प्रकार|2 Videosपरवलय
JEE Main & Advanced (Hindi Medium)|Exercise रिक्त स्थानों की पूर्ति कीजिये|1 Videosनिश्चित समाकलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णाक प्रश्न|7 Videosप्रतिलोम वृत्तीय फलन
JEE Main & Advanced (Hindi Medium)|Exercise एकल पूर्णांक प्रश्न|1 Videos
JEE Main & Advanced (Hindi Medium)-परवलय-श्रृंख्लाबद्ध बोधन प्रकार
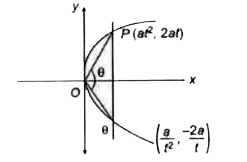
- माना कि PQ परवलय y^(2)=4ax की एक नाभीय जीवा है। बिन्दुओं P तथा Q पर पर...
Text Solution
|
- माना कि PQ परवलय y^2=4ax की एक नाभीय जीवा है। बिन्दुओं P तथा Q पर परव...
Text Solution
|
- माना कि a,r, s, t शून्येतर वास्तविक संख्याये (non zero real numbers) ह...
Text Solution
|
- माना कि a,r, s, t शून्येतर वास्तविक संख्याये (non zero real numbers) ह...
Text Solution
|