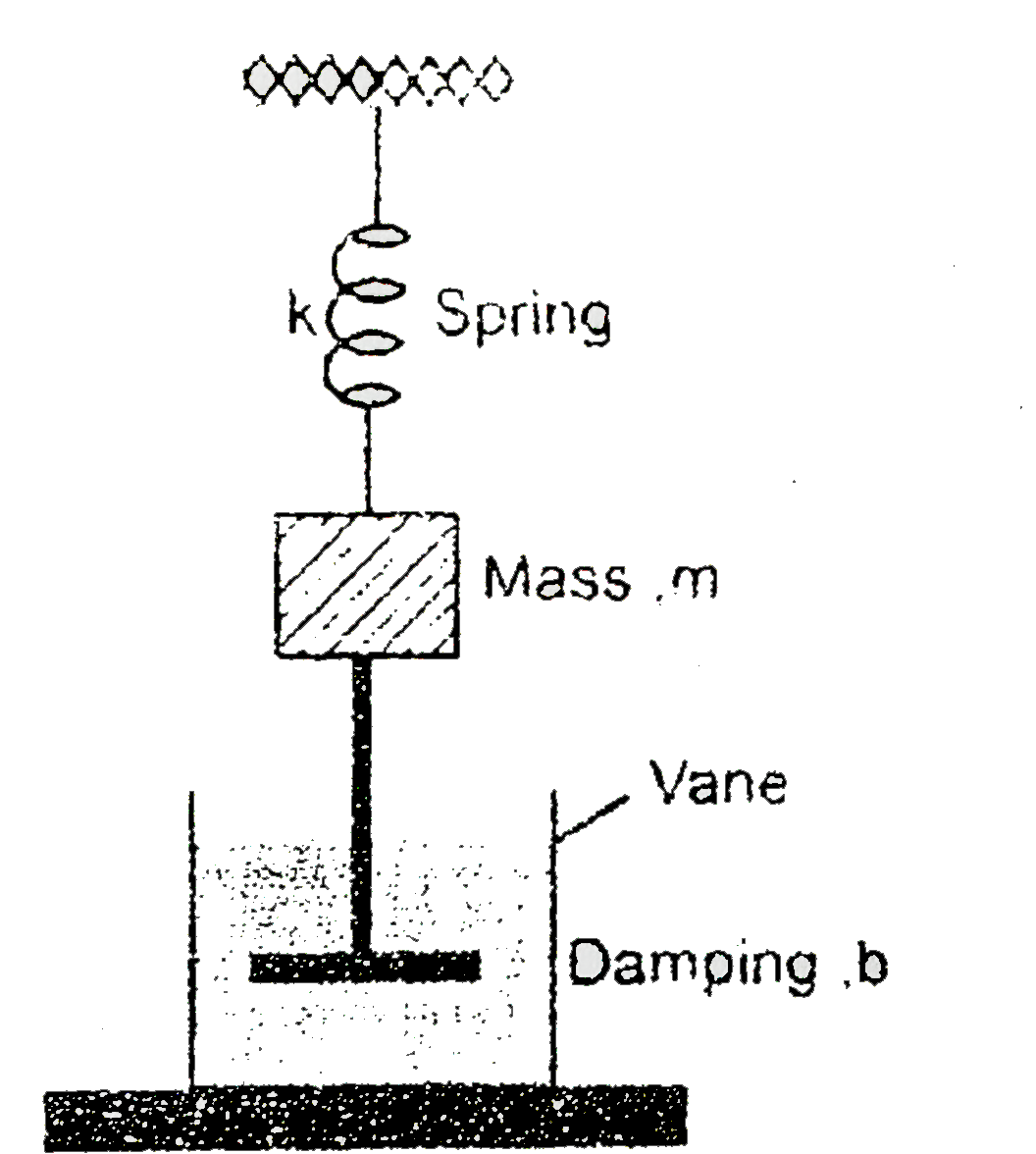Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
RESONANCE|Exercise Exercise- 1, PART - II|37 VideosSIMPLE HARMONIC MOTION
RESONANCE|Exercise Exercise- 2, PART - I|26 VideosSIMPLE HARMONIC MOTION
RESONANCE|Exercise Board Level Exercise|24 VideosSEMICONDUCTORS
RESONANCE|Exercise Exercise 3|88 VideosTEST PAPERS
RESONANCE|Exercise FST-3|30 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 1, PART - I
- For the damped oscillator shown in Fig, the mass of the block is 200 g...
Text Solution
|
- The equation of a particle executing SHM is x = (5m)[(pis^(-1))t + (pi...
Text Solution
|
- A particle having mass 10 g oscilltes according to the equatioi (x=(2....
Text Solution
|
- A simple harmonic motion has an amplitude A and time period T. Find th...
Text Solution
|
- At particle is executing SHM with amplitude A and has maximum velocity...
Text Solution
|
- A particle executes simple harmonic motion with an amplitude of 10 cm ...
Text Solution
|
- A particle is executing SHM. Find the positions of the particle where ...
Text Solution
|
- A particle performing SHM with amplitude 10cm. At What distance from m...
Text Solution
|
- An object of mass 0.2 kg executes simple harmonic oscillation along th...
Text Solution
|
- A spring mass system has time period of 2 second. What should be the s...
Text Solution
|
- A body of mass 2 kg suspended through a vertical spring executes simpl...
Text Solution
|
- A vertical spring-mass system with lower end of spring is fixed, made ...
Text Solution
|
- The spring shown in figure is unstretched when a man starts pulling on...
Text Solution
|
- Three spring mass systems are shown in figure. Assuming gravity free s...
Text Solution
|
- Spring mass system is shown in figure. Find the elastic potential ener...
Text Solution
|
- Find the length of seconds pendulum at a place where g = pi^(2) m//s^(...
Text Solution
|
- Instantaneous angle (in radian) between string of a simple pendulum an...
Text Solution
|
- A pendulum clock giving correct time at a place where g=9.800 ms^-2 is...
Text Solution
|
- A pendulum is suspended in a lit and its period of oscillation is T(0)...
Text Solution
|
- Compound pendulum are made of : (a) A rod of length l suspended thro...
Text Solution
|
- A uniform disc of radius r is to be suspended through a small hole mad...
Text Solution
|