Home
Class 12
MATHS
Solver sin^(-1) x gt tan^(-1) x...

Solver `sin^(-1) x gt tan^(-1) x`

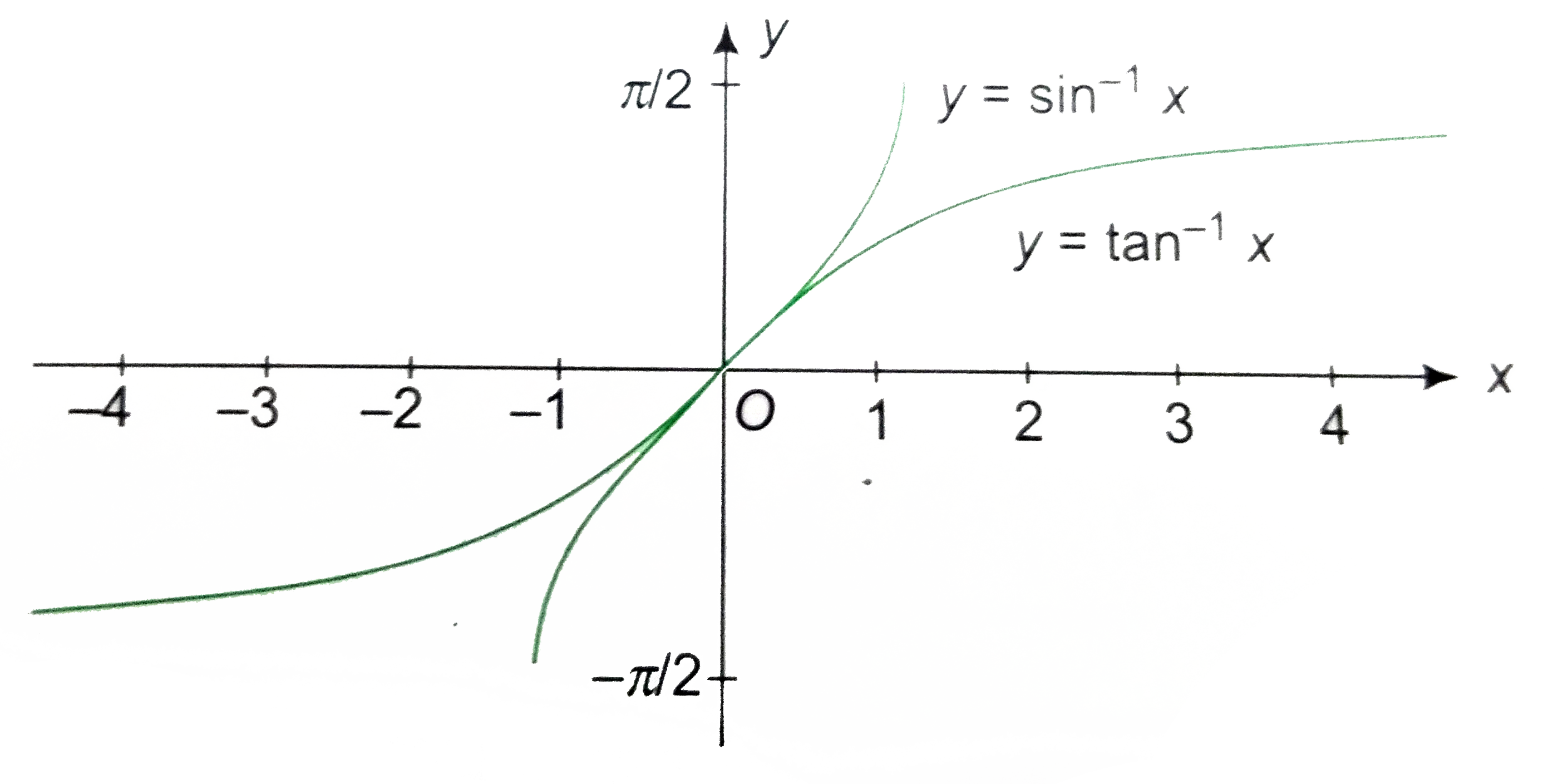
Text Solution

Verified by Experts

The correct Answer is:
`x in (0,1)`
We have `sin^(-1) x lt tan^(-1) x`
Given inequality is meaningful if `x in [-1, 1]`.
Now, let's draw the graph of `y = sin^(-1) x and y = tan^(-1) x`.

From the graph, we can see that `sin^(-1) x gt tan^(-1) x " for " x in (0, 1]`
Promotional Banner

Topper's Solved these Questions

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise 7.2|6 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Exercise 7.3|12 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    CENGAGE|Exercise Question Bank|24 Videos

  • INTRODUCTION TO VECTORS

    CENGAGE|Exercise JEE Previous Year|20 Videos

  • JEE 2019

    CENGAGE|Exercise Chapter 10|9 Videos

Similar Questions

Explore conceptually related problems

Solver sin^(-1) x gt -1

Solve tan^(-1) x gt cot^(-1) x

If sin^(-1) x gt cos^(-1) x then

Prove that tan^(-1) x + tan ^(-1). 1/x = {{:(pi//2", if " x gt 0),(-pi//2", if "x lt 0 ):} .

Prove that sin cot^(-1) tan cos^(-1) x = sin cosec^(-1) cot tan^(-1) x = x, " where " x in [0,1]

Let x_(1) " and " x_(2) ( x_(1) gt x_(2)) be roots of the equation sin^(-1) ( cos ( tan^(-1)( cosec ( cot^(-1)x)))) = pi/6 , then

If x + y + z = xyz and x, y, z gt 0 , then find the value of tan^(-1) x + tan^(-1) y + tan^(-1) z

solve sin^(-1) (sin 5) gt x^(2) - 4x