Home
Class 12
MATHS
Draw the graph of the function: Solve |(...

Draw the graph of the function: Solve `|(x^2)/(x-1)|lt=1` using the graphical method.

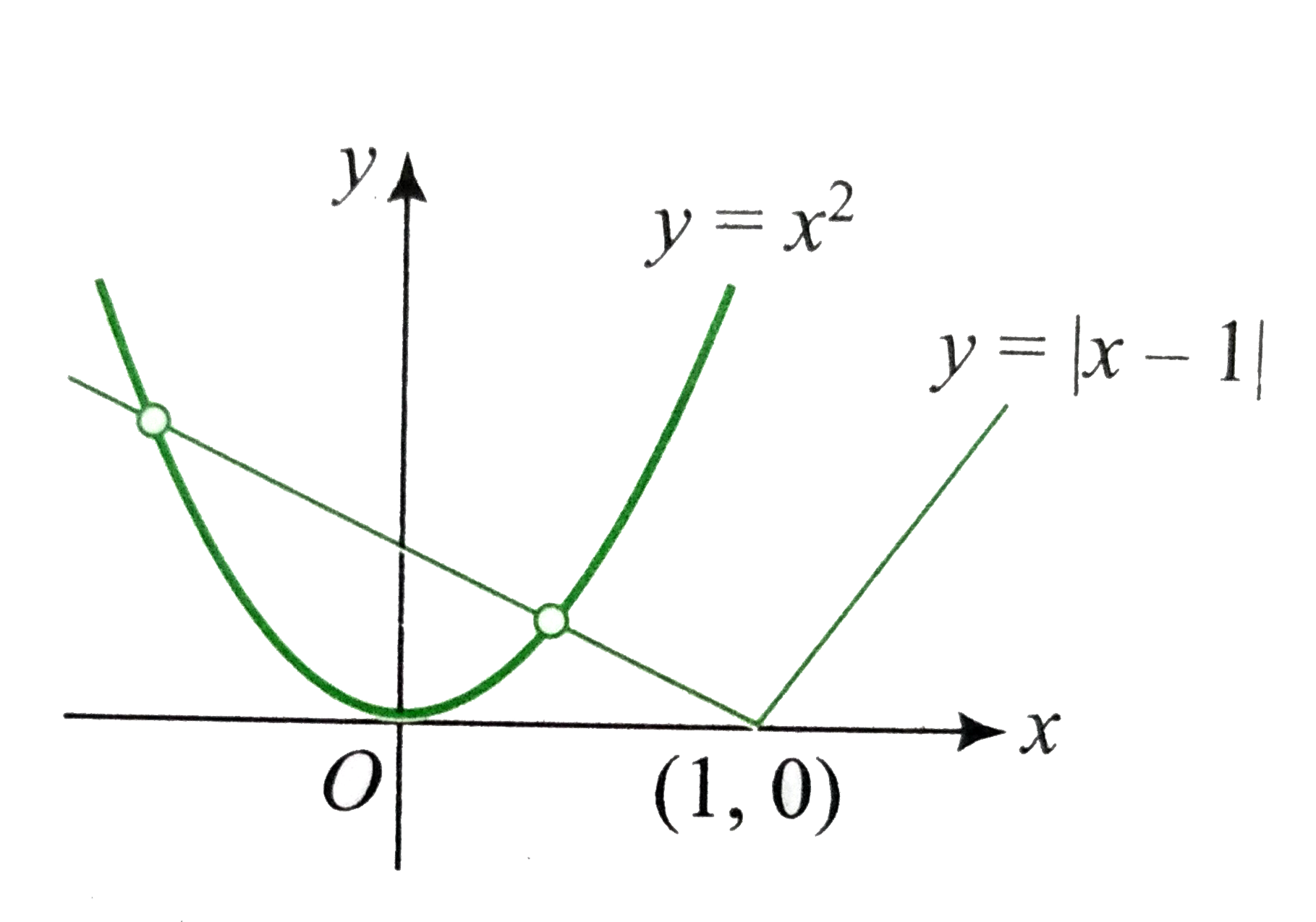
Text Solution

Verified by Experts

`|(x^(2))/(x-1)| le 1 " or " x^(2) le |x-1|, x ne 1`

The figure represents the graph of `y=x^(2) " and " y=|x-1|.`
Solving `x^(2)=1-x,` we get `x=(-1+-sqrt(5))/(2).`
Thus, the solution is `[(-1-sqrt(5))/(2),(-1+sqrt(5))/(2)]`.
Promotional Banner

Topper's Solved these Questions

  • RELATIONS AND FUNCTIONS

    CENGAGE|Exercise Exercise (Single)|125 Videos

  • RELATIONS AND FUNCTIONS

    CENGAGE|Exercise Exercise (Multiple)|27 Videos

  • RELATIONS AND FUNCTIONS

    CENGAGE|Exercise Exercise 1.14|13 Videos

  • Quadratic Equations, Inequalities, Modulus and Logarithms

    CENGAGE|Exercise Question Bank|31 Videos

  • SCALER TRIPLE PRODUCTS

    CENGAGE|Exercise DPP 2.3|11 Videos

Similar Questions

Explore conceptually related problems

Draw the graph of the function: Solve |(x^(2))/(x-1)|<=1 using the graphical method.

Draw the graph of the function: 1-x

Draw the graph of the function f(x)=x^(x)

Draw the graph of the function: f(x)=|x^(2)-3|x|+2|

Draw the graph of the function: f(x)=-|x-1|^((1)/(2))

Draw the graph of the function f(x) = (1+1/x)^(2)

Draw the graph of the function f(x) =|x|+| x-1|

Draw graph of x lt -y

Solve : (x +2)/(x+1)lt 0