Home
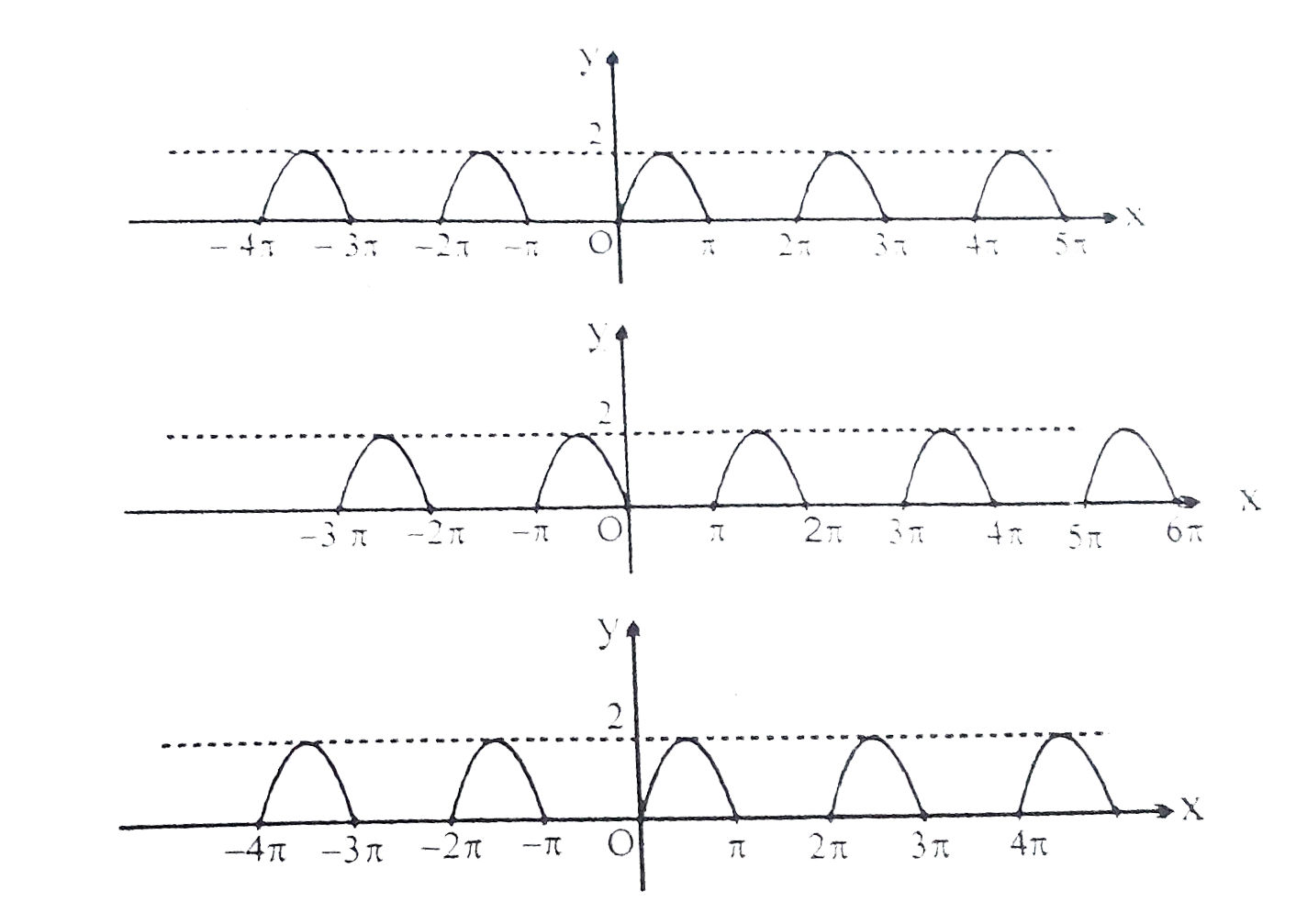
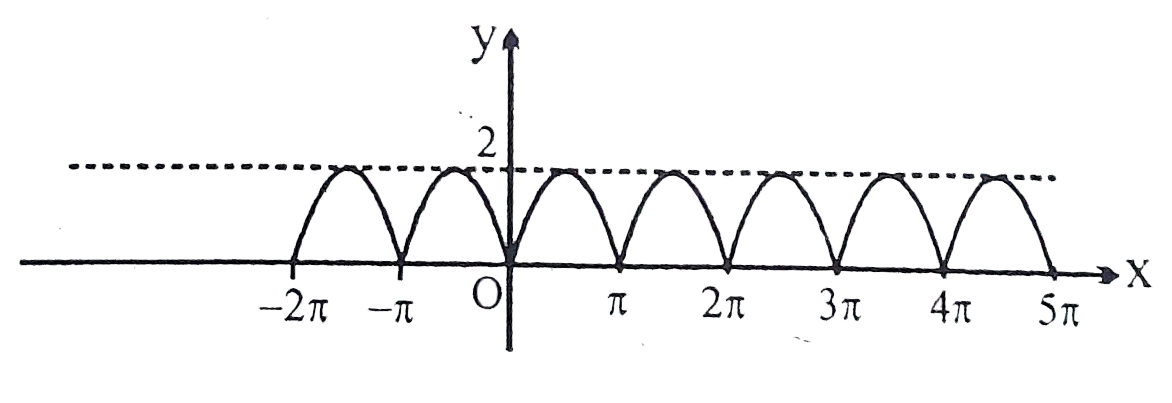
Class 12
MATHS
If f(x)=sinx+|sinx|andg(x)=f(x-pi)+f(x+2...

If `f(x)=sinx+|sinx|andg(x)=f(x-pi)+f(x+2pi)`, then value of `underset(-2pi)overset(5pi)(f)g(x)dx` is

A

15

B

7

C

12

D

28

Text Solution

Verified by Experts

The correct Answer is:
A

`:." "g(x)=f(x-pi)+f(x+2pi)`

`underset(-2pi)overset(5pi)(f)g(x)dx`
`:." required area"=2[2xx7]=28`.
Aliter : `g(x)=f(x-pi)+f(x+2pi)=(-sinx+|sinx|)+(sinx|sinx|)rArrg(x)=2|sinx|`
`"So, "underset(-2pi)overset(5pi)(f)g(x)dx=28`.
Promotional Banner

Topper's Solved these Questions

  • TEST PAPERS

    BANSAL|Exercise MATHS SECTION-3 PART-B [MULTIPLE CORRECT CHOICE TYPE]|5 Videos

  • TEST PAPERS

    BANSAL|Exercise MATHS SECTION-3 PART-C [INTEGER TYPE]|5 Videos

  • TEST PAPERS

    BANSAL|Exercise CHEMISTRY SECTION-2 PART-C [INTEGER TYPE]|5 Videos

  • PROBABILITY

    BANSAL|Exercise All Questions|1 Videos

  • THERMODYNAMICS

    BANSAL|Exercise Match the column|7 Videos

Similar Questions

Explore conceptually related problems

If f(x)=x+sin x, then find the value of int_(pi)^(2 pi)f^(-1)(x)dx

If f(x) = 2 sinx, g(x) = cos^(2) x , then the value of (f+g)((pi)/(3))

If f(x)=cos ec(x-(pi)/(3))cos ec(x-(pi)/(6)) then the value of int_(0)^((pi)/(2))f(x)dx is

If f(x)=(2-xcosx)/(2+xcosx)andg(x)= "log"_(e)x, (xgt0) then the value of the integral int_(-pi//4)^(pi//4)g(f(x)) dx is

If f(x)=int(sinx)/(cos^(2)x)(1-3sin^(3)x)dx , then value of (f(0)-f(pi)+(9pi)/2) is

Let f(x)=|x|+|sinx|, x in (-pi/ 2,3pi/2). Then , f is

f(x)=sinx+int_(-pi//2)^(pi//2)(sinx+tcosx)f(t)dt The value of int_(0)^(pi//2) f(x)dx is