Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-COLLISION -(NUMERICAL BASED QUESTIONS)
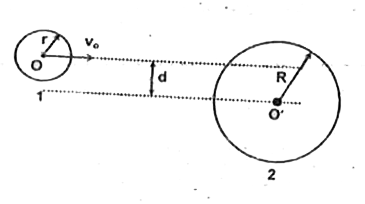
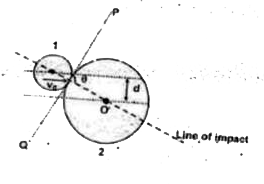
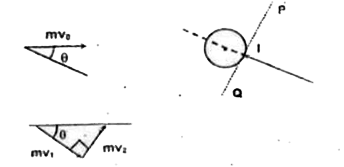
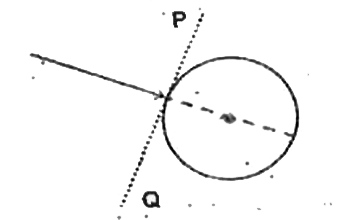
- A disc of mass m is moving with constant speed v(0) on a smooth horizo...
Text Solution
|
- A ball is projected from the floor of a cabin of height 7m with speed ...
Text Solution
|
- A man of mass m is moving with a constant acceleration a w.r.t. plank....
Text Solution
|
- A sphere of mass m is moving with a velocity (4 hat(i)-hat(j)) m/s hit...
Text Solution
|
- Two ladders are hanging from ands of a light rope passing over a light...
Text Solution
|