Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
FIITJEE|Exercise SOLVED PROBLEMS ( OBJECTIVE)|15 VideosELECTROMAGNETIC INDUCTION
FIITJEE|Exercise Comprehension Based Type Comprehension -I|3 VideosELECTROMAGNETIC INDUCTION
FIITJEE|Exercise EXERCISE|9 VideosELASTICITY AND WAVES
FIITJEE|Exercise Assignment Problems (Objective) Level-II|15 VideosELECTROMAGNETIC INDUCTION AND AC CURRENT
FIITJEE|Exercise Example|15 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-ELECTROMAGNETIC INDUCTION-SOLVED PROBLEMS ( SUBJECTIVE)
- A metallic rod of mass m length R is pivoted at O. It is free to rotat...
Text Solution
|
- An infinitesimal bar magnet of dipole moment M is pointing and moving ...
Text Solution
|
- A conducting bar of mass m length l is pushed with a speed V(0) on a ...
Text Solution
|
- There is a the system of two concentric loops of radii r and R (R gt g...
Text Solution
|
- Shown in the figure is a parallel R , L,C circuit with key K(1) closed...
Text Solution
|
- A long solid cylindrical straight conductor carries a current i(0) . F...
Text Solution
|
- A metal disc of radius R resistivity rho thickness y is subjected into...
Text Solution
|
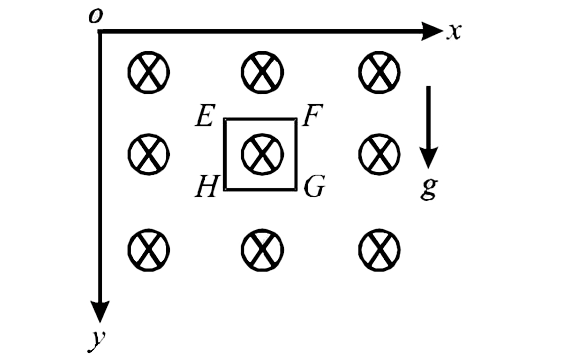
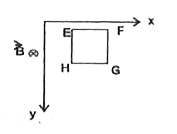
- A magnetic field B = B(0) (y//a)(hat)k is into the paper in the +z dir...
Text Solution
|
- A thermocol vessel contains 0.5kg of distilled water at 30^(@)C. A me...
Text Solution
|
- Two infinite parallel wire, having the cross sectional area 'a' and re...
Text Solution
|