Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATIONS OF DERIVATIVES
RS AGGARWAL|Exercise Exercise 11B|17 VideosAPPLICATIONS OF DERIVATIVES
RS AGGARWAL|Exercise Exercise 11C|27 VideosAPPLICATIONS OF DERIVATIVES
RS AGGARWAL|Exercise Objective Questions|89 VideosADJOINT AND INVERSE OF A MATRIX
RS AGGARWAL|Exercise Exercise 7|37 VideosAREA OF BOUNDED REGIONS
RS AGGARWAL|Exercise Exercise 17|39 Videos
Similar Questions
Explore conceptually related problems
RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Exercise 11A
- The radius of a circle is increasing at the rate of 0.7 cm/sec. Wha...
Text Solution
|
- The radius of a circle is increasing uniformly at the rate of 0.3 cent...
Text Solution
|
- The side of a square sheet of metal is increasing at 3 centimetres per...
Text Solution
|
- The radius of a spherical soap bubble is increasing at the rate of ...
Text Solution
|
- The radius of an air bubble is increasing at the rate of 0.5 cm/sec...
Text Solution
|
- The volume of a spherical balloon is increasing at a rate of 25 cm^(3...
Text Solution
|
- A balloon which always remains spherical, is being inflated by pump...
Text Solution
|
- The bottom of a rectangular swimming tank is 25 m by 40m. Water is pum...
Text Solution
|
- A stone is dropped into a quiet lake and waves move in circles at a sp...
Text Solution
|
- A man 2 metres high walks at a uniform speed of 5 km/hr away from a ...
Text Solution
|
- An inverted cone has a depth of 40 cm and a base of radius 5 cm. Water...
Text Solution
|
- Sand is pouring from a pipe at the rate of 18 cm^(3)//s. The falling s...
Text Solution
|
- Water is dripping out from a conical funnel at a uniform rate of 4c m^...
Text Solution
|
- Oil is leaking at the rate of 16 mL/s from a vertically kept cylindric...
Text Solution
|
- A 13-m long ladder is leaning against a wall. The bottom of the ladder...
Text Solution
|
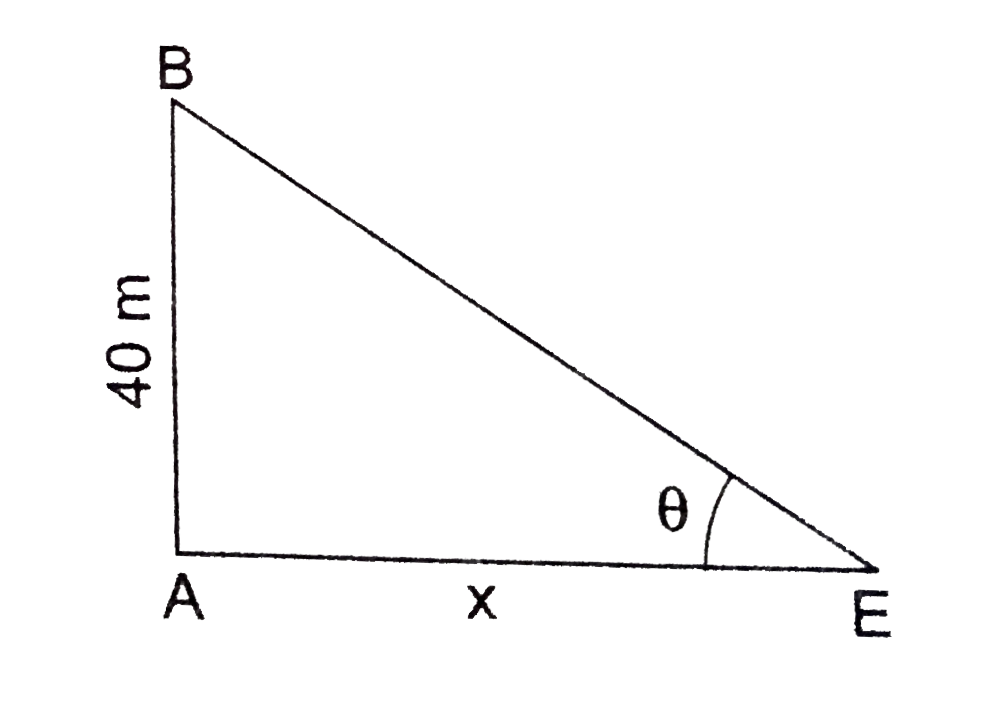
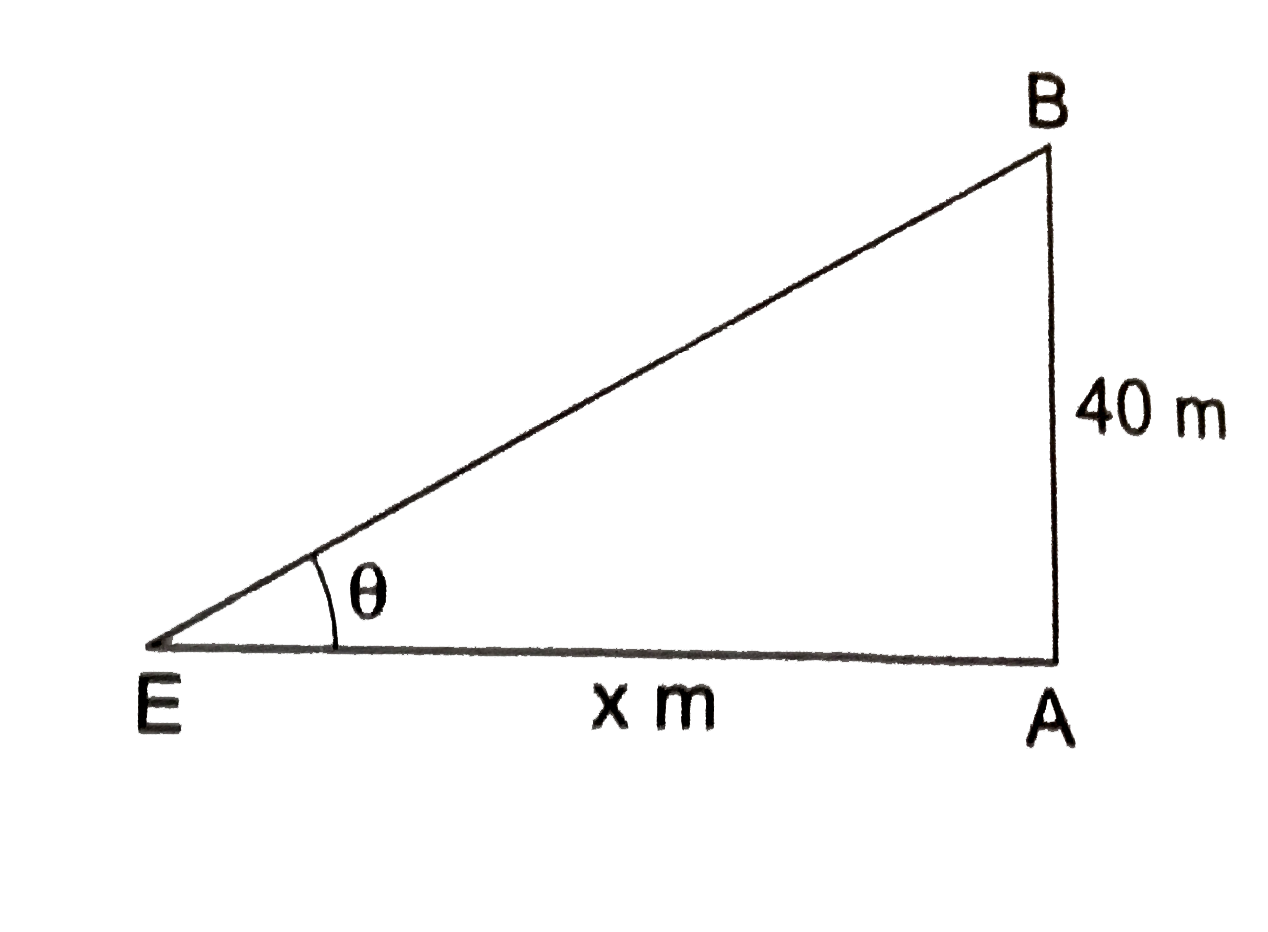
- A man is moving away from a 40-m high tower at a speed of 2 m/s. Find ...
Text Solution
|
- Find an angle theta,0<theta<theta<pi/2, which increases twice as fast ...
Text Solution
|
- The radius of a balloon is increasing at the rate of 10 cm/sec. At ...
Text Solution
|
- An edge of a variable cube is increasing at the rate of 5 cm/s. How fa...
Text Solution
|
- The sides of an equilateral triangle are increasing at the rate of ...
Text Solution
|