Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RS AGGARWAL-SCALAR, OR DOT, PRODUCT OF VECTORS-Exercise 23
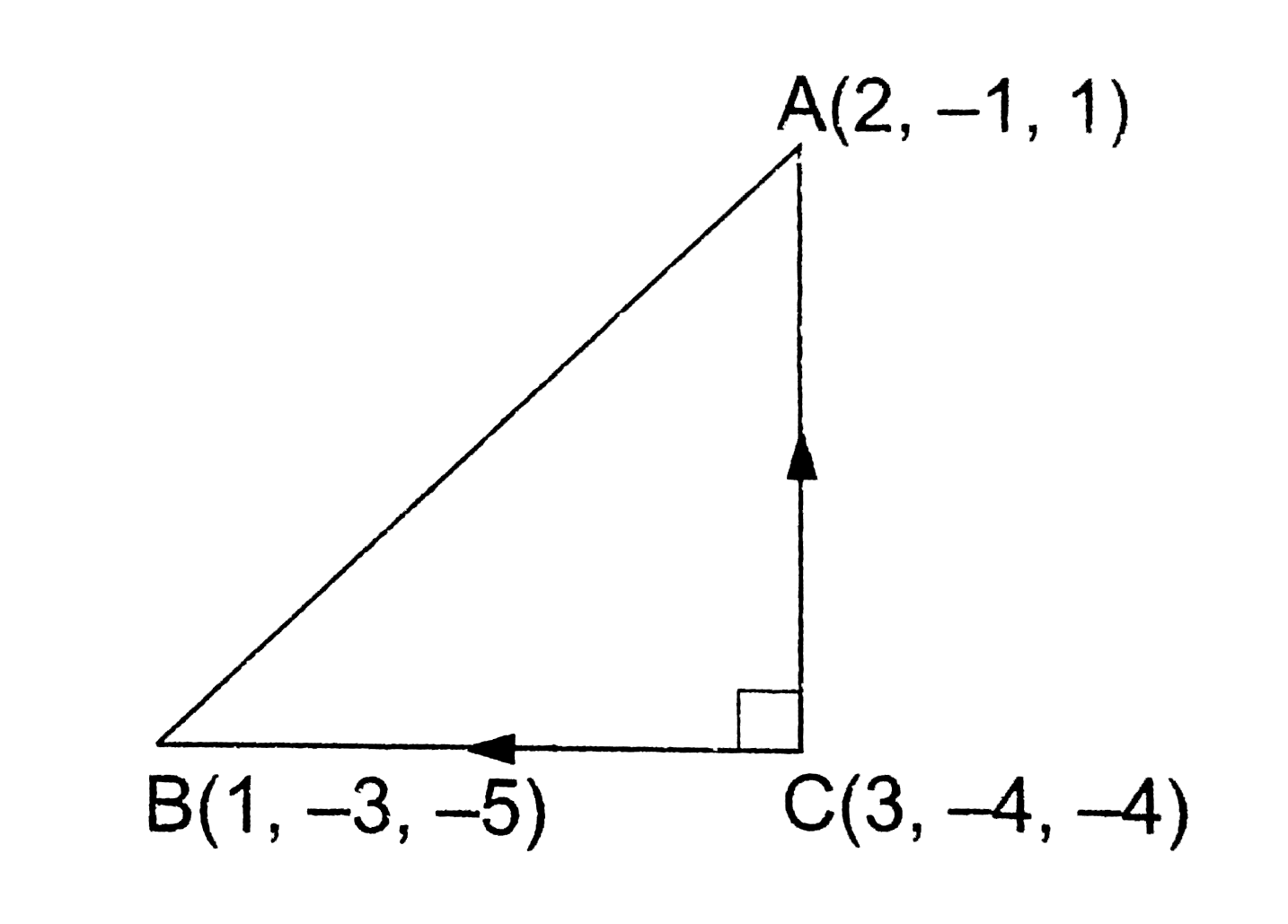
- Show that the points, A, B and C having position vectors (2hat(i)-hat(...
Text Solution
|
- Find vec(a).vec(b) when (i) vec(a)=hat(i)-2hat(j)+hat(k) and vec(b)=...
Text Solution
|
- Find the value of lambda for which vec(a) and vec(b) are perpendicular...
Text Solution
|
- (i) If vec(a)=hat(i)+2hat(j)-3hat(k) and vec(b)=3hat(i)-hat(j)+2hat(k)...
Text Solution
|
- If vec a= hat a= hat i-\ hat j+7 hat k and vec b=5 hat j-\ hat j+l...
Text Solution
|
- Show that the vectors vec a=1/7(2 hat i+3 hat j+6 hat k), vec b=1/7(3...
Text Solution
|
- Let vec(A)=4hat(i)+5hat(j)-hat(k), vec(b)=hat(i)-4hat(j)+5hat(k) and v...
Text Solution
|
- Let vec(a)=(2hat(i)+3hat(j)+2 hat(k)) and vec(b)=(hat(i)+2hat(j)+hat(k...
Text Solution
|
- Find the projection of (8hat(i)+hat(j)) in the direction of (hat(i)+2h...
Text Solution
|
- Write the projection of vector hat i+ hat j+ hat k along the vector ...
Text Solution
|
- (i) Find the projection of vec(a) on vec(b) if vec(a).vec(b)=8 and vec...
Text Solution
|
- Find the angle between the vectors vec(a) and vec(b), when (i) vec(a...
Text Solution
|
- If vec(a)=(hat(i)+2hat(j)-3hat(k)) and vec(b)=(3hat(i)-hat(j)+2hat(k))...
Text Solution
|
- if veca is a unit vector and (vecx-veca).(vecx+veca)=8 then |vecx|
Text Solution
|
- Find the angles which the vector vec(a)=3 hat(i)-6hat(j)+2hat(k) makes...
Text Solution
|
- Show that the vector hat i+ hat j+ hat k is equally inclined with the...
Text Solution
|
- Find a vector vec a of magnitude 5sqrt(2) making an angle pi/4 with x-...
Text Solution
|
- Find the angle between (vec(a)+vec(b)) and (vec(a)-vec(b)), if vec(a)=...
Text Solution
|
- Express the vector vec(a)=(6hat(i)-3hat(j)-6hat(k)) as sum of two vect...
Text Solution
|
- Prove that ( -> a+ -> b)dot( -> a+ -> c)| -> a|^2+| -> b|^2 , if and o...
Text Solution
|
- If vec a+ vec b+ vec c=0,| vec a|=3,| vec b|=5,| vec c|=7, then find ...
Text Solution
|