Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT BANGLISH-CIRCLES-EXERCISE 12.3
- Draw the following triangle. In Delta ABC , AB= 6cm, BC = 7cm " and...
Text Solution
|
- Draw the following triangles . in Delta PQR, PQ = 5cm , QR = 6cm " ...
Text Solution
|
- Draw the following triangle In Delta XYZ, XY = 4.8 cm , angle X = 60...
Text Solution
|
- Draw circle passing through A, B where AB = 5.4cm
Text Solution
|
- If two circles intersect at two points, then prove that their centres ...
Text Solution
|
- If two intersecting chords of a circle make equal angles with diameter...
Text Solution
|
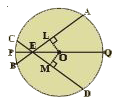
- In the adjacent figure, AB is a chord of circle with centre O. CD is t...
Text Solution
|