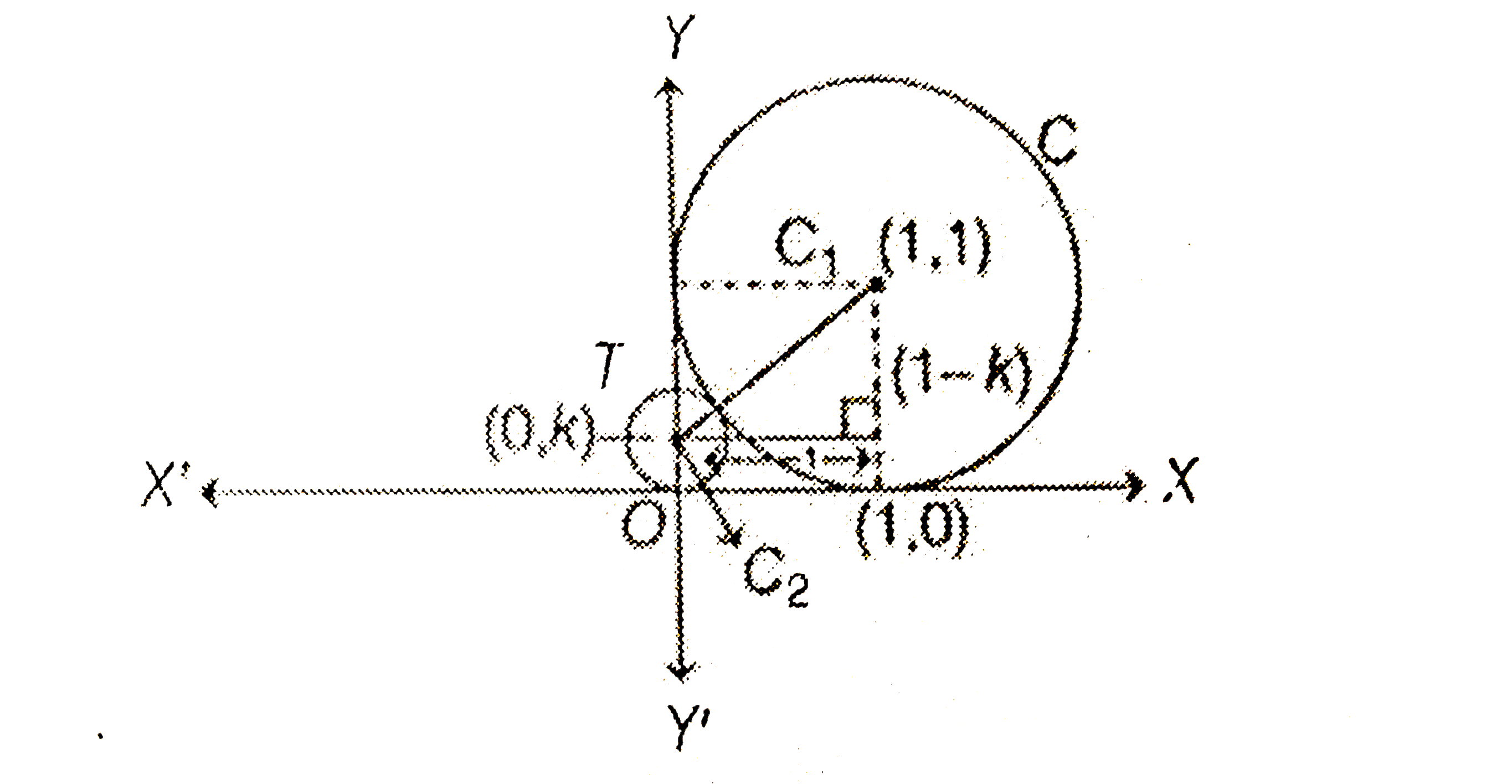A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 2 Objective Question II|2 VideosCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 2 Passage Based Problems|3 VideosCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 1 Paragraph Based Questions|2 VideosBINOMIAL THEOREM
IIT JEE PREVIOUS YEAR|Exercise Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )|8 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)|1 Videos
IIT JEE PREVIOUS YEAR-CIRCLE-Topic 2 Relation between Two Circles
- If the circles x^(2)+y^(2) +5Kx+2y + K=0 and2(x^(2)+y^(2))+2Kx +3y...
Text Solution
|
- If a tangent to the circle x^(2)+y^(2)=1 intersects the coordinate axe...
Text Solution
|
- If a variable line, 3x + 4y -lambda = 0 is such that the two circles x...
Text Solution
|
- Let x^2 +y^2 -2x-2y-2=0 and x^2 +y^2 -6x-6y+14=0 are two circles C1, C...
Text Solution
|
- If the circles x^(2)+y^(2) +5Kx+2y + K=0 and2(x^(2)+y^(2))+2Kx +3y...
Text Solution
|
- If one of the diameters of the circle, given by the equation, x^2+y^2-...
Text Solution
|
- If one of the diameters of the circle x^2+y^2-2x-6y+ 6 = 0 is a chord ...
Text Solution
|
- The number of common tangents to the circles "x"^("2")"+y"^("2")"-4x...
Text Solution
|
- Let C be the circle with centre at (1, 1) and radius = 1. If T is th...
Text Solution
|
- If the circles x^2+y^2+2x+2ky+6=0 and x^2+y^2+2ky+k=0 intersect ortho...
Text Solution
|
- An acute triangle PQR is inscribed in the circle x^2+y^2= 25. If Q and...
Text Solution
|
- The number of common tangents to the circles x^(2) + y^(2) = 4 and x^...
Text Solution
|
- The angle between a pair of tangents from a point P to the circe x^2 +...
Text Solution
|
- If the two circles (x+1)^2+(y-3)=r^2 and x^2+y^2-8x+2y+8=0 intersect i...
Text Solution
|
- If a circle passes through the point (a, b) and cuts the circle x^2 +y...
Text Solution
|