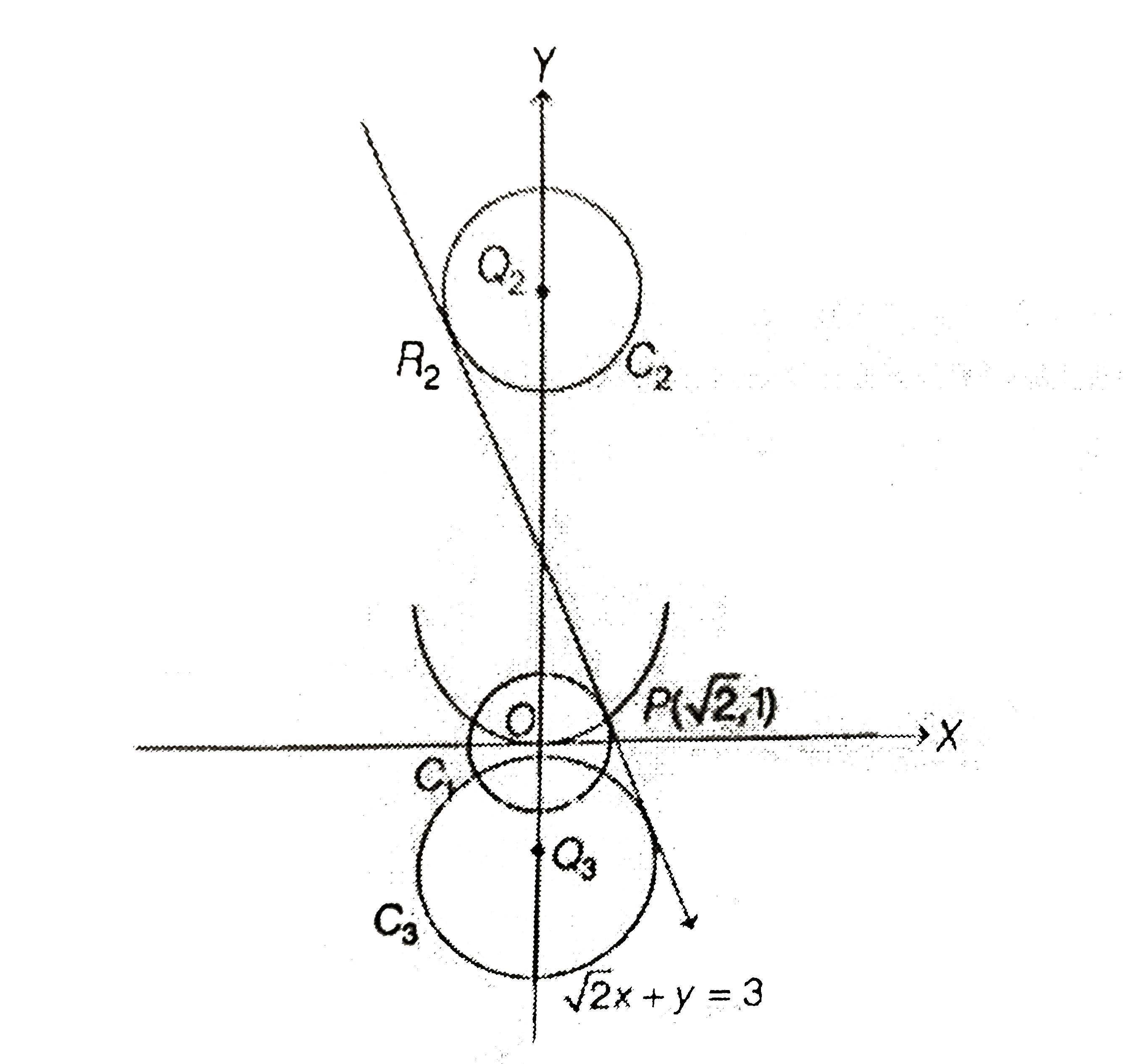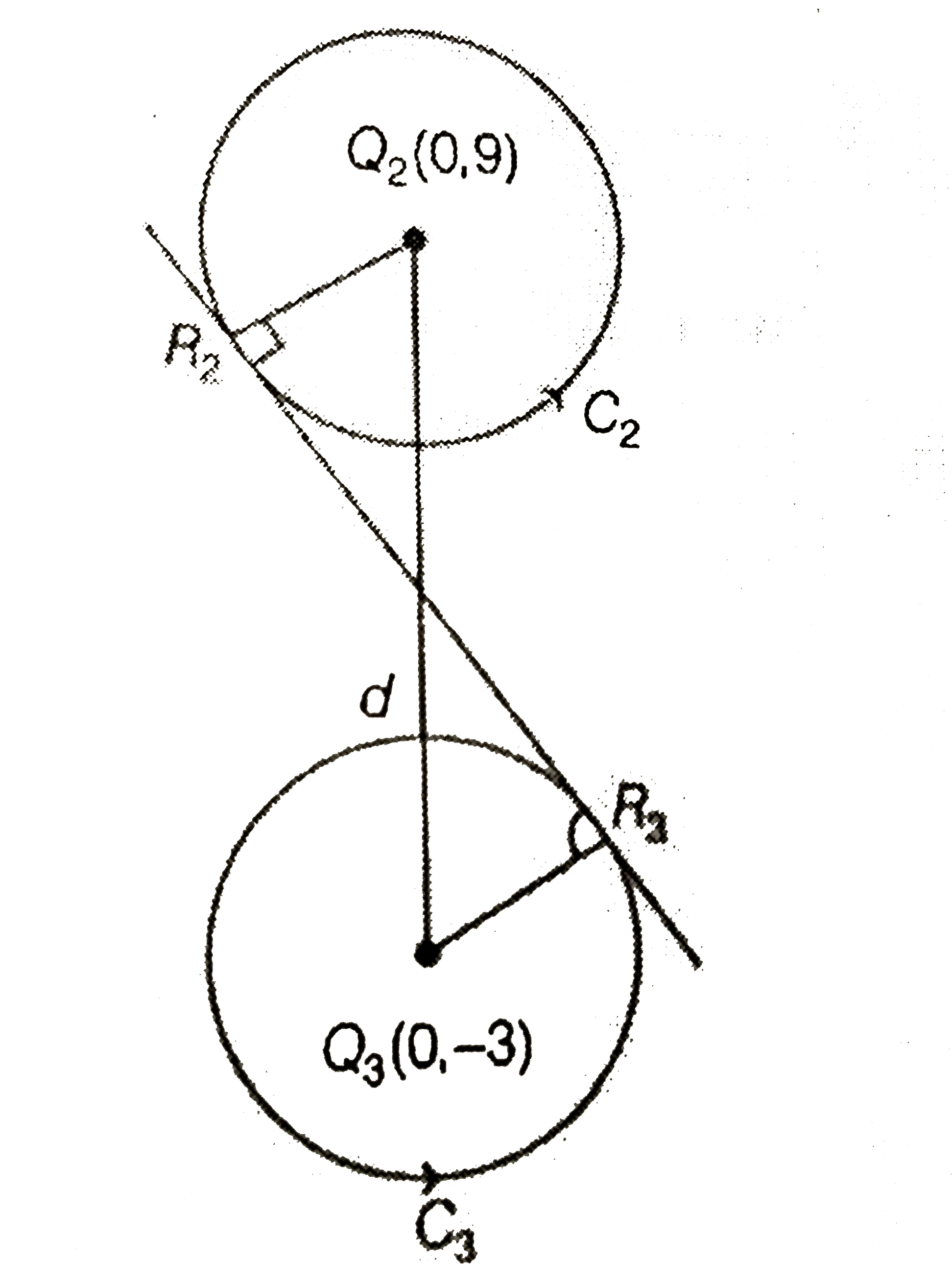Home
Class 12
MATHS
The circle C1 : x2 + y2 = 3, with centre...

The circle C1 : x2 + y2 = 3, with centre at O, intersects the parabola x2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii 2 3 and centres Q2 and Q3, respectively.

A

`Q_(2)Q_(3)= 12`

B

`R_(2)R_(3)= 4sqrt6`

C

area of the `DeltaPR_(2)R_(3) " is " 6sqrt2`

D

area of the `DeltaPQ_(2)Q_(3)" is " 4sqrt2`

Text Solution

Verified by Experts

The correct Answer is:
A, B, C
Given `C_(1):x^(2)+y^(2)=3` intersects the parabola `x^(2)=2y`.

On solving `x^(2)+y^(2)=3 and x^(2)=2y`, we get
`y^(2)+2y=3`
`rArr y^(2)+2y-3=0`
`rArr (y+3)(y-1)=0`
`therefore y=1, -3["neglecting " y=-3, as -sqrt3leylesqrt3]`
`therefore y=1 rArrx=pmsqrt2`
`rArr P(sqrt2,1) in "I quadrant"`
Equation of tangent at `Psqrt2,1)"to " C_(1):x^(2)+y^(2)=3` is
`sqrt2x+1*y=3" "...(i)`
Now, let the centres of `C_(2) and C_(3)` at `R_(2) and R_(3)` shown as below

Let `Q_(2)` be (0,k) and radius is `2sqrt3`.
`therefore (|0+k-3|)/(sqrt(2+1))=2sqrt3`
`rArr |k-3|=6`
`rArr h=9, -3`
`therefore Q_(2)(0,9) and Q_(3)(0,-3)`
Hence, `Q_(2)Q_(3)=12`
`therefore` option (a) is correct.
Also, `R_(2)R_(3)` is common internal tangent to `C_(2) and C_(3)`,
and `r_(2)=r_(3)=2sqrt3`
`R_(2)R_(3)=sqrt(d^(2)-(r_(1)+r_(2 ))^(2))=sqrt(12^(2)-(4sqrt3)^(2))`
`=sqrt(144-48)=sqrt96=4sqrt6`

`therefore` (b) is correct.
`therefore` Length of perpendicular from `O(0,0) "to " R_(2)R_(3)` is equal to radius of `C_(1)=sqrt3`
`therefore " Area of " DeltaPQ_(2)Q_(3)=(1)/(2)Q_(2)Q_(3)xxsqrt2=(sqrt2)/(2)xx12=6sqrt2`
`therefore` Option (c) is correct.
Also, area of `DeltaPQ_(2)Q_(3)=(1)/(2)Q_(2)Q_(3)xxsqrt2=(sqrt2)/(2)xx12=6sqrt2`
`therefore` Option (d) is incorrect.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    IIT JEE PREVIOUS YEAR|Exercise Topic 3 Assertion and Reason|1 Videos

  • CIRCLE

    IIT JEE PREVIOUS YEAR|Exercise Topic 3 Passage Based Problems (passage 1)|3 Videos

  • CIRCLE

    IIT JEE PREVIOUS YEAR|Exercise Topic 3 Equation of Tangent, Normal and Length of Tangents|9 Videos

  • BINOMIAL THEOREM

    IIT JEE PREVIOUS YEAR|Exercise Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )|8 Videos

  • COMPLEX NUMBERS

    IIT JEE PREVIOUS YEAR|Exercise TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)|1 Videos

Similar Questions

Explore conceptually related problems

The circle C_1 : x^2 + y^2 = 3, with centre at O, intersects the parabola x^2 = 2y at the point P in the first quadrant. Let the tangent to the circle C_1 at P touches other two circles C_2 and C_3 at R_2 and R_3, respectively. Suppose C_2 and C_3 have equal radii 2sqrt3 and centres at Q_2 and Q_3 respectively. If Q_2 and Q_3 lie on the y-axis, then (a) Q2Q3= 12(b)R2R3=4sqrt6(c)area of triangle OR2R3 is 6sqrt2 (d)area of triangle PQ2Q3 is= 4sqrt2

The circle C_(1) : x^(2)+y^(2)=3 , with cenre at O, intersects the parabola x^(2)=2y at the point P in the first quadrant. Let the tangent to the circle C_(1) at P touches other two circles C_(2) and C_(3) at R_(2) and R_(3) respectively. Suppose C_(2) and C_(3) have equal radii 2sqrt(3) and centres Q_(2) and Q_(3) respectively. If Q_(2) and Q_(3) lie on the y-axis, then Q_(2)Q_(3)=

A circle with centre at (15,-3) is tangent to y=(x^(2))/(3) at a point in the first quadrant.The radius of the circle is equal to

Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They intersect at P and Q in first and 4th quadrant,respectively. Tangents to the circle at P and Q intersect the x-axis at R and tangents at the parabola at P and Q intersect the x-axis at S.

Consider the circle x^2+y^2=9 and the parabola y^2=8x . They intersect at P and Q in the first and fourth quadrants, respectively. Tangents to the circle at P and Q intersect the X-axis at R and tangents to the parabola at P and Q intersect the X-axis at S. The ratio of the areas of trianglePQS" and "trianglePQR is

A line y=2x+c intersects the circle x^(2)+y^(2)-2x-4y+1=0 at P and Q. If the tangents at P and Q to the circle intersect at a right angle,then |c| is equal to

Let the line L : sqrt(2)x y =alpha pass through the point of the intersection P (in the first quadrant) of the circle x^2 y^2 = 3 and the parabola x^2 = 2y . Let the line L touch two circles C_1 and C_2 of equal radius 2 sqrt 3 . If the centres Q_1 and Q_2 of the circles C_1 and C_2 lie on the y-axis, then the square of the area of the triangle PQ_1Q_2 is equal to ___________.

A circle C touches the line x = 2y at the point (2, 1) and intersects the circle C_1 : x^2 + y^2 + 2y -5 = 0 at two points P and Q such that PQ is a diameter of C^1 . Then the diameter of C is :