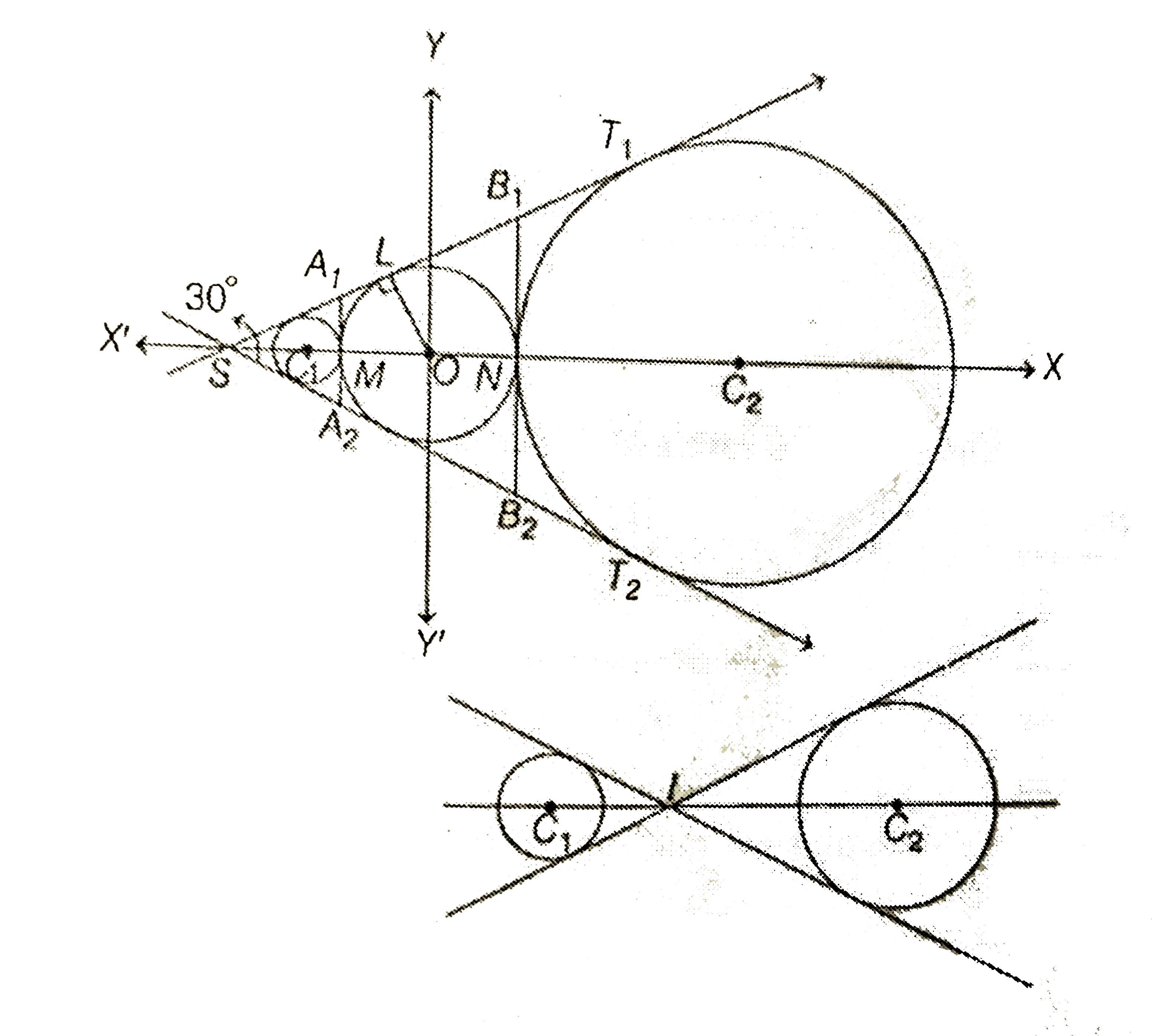Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 5 Integer Answer type Question|1 VideosCIRCLE
IIT JEE PREVIOUS YEAR|Exercise Topic 5 Fill in the blanks|7 VideosBINOMIAL THEOREM
IIT JEE PREVIOUS YEAR|Exercise Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )|8 VideosCOMPLEX NUMBERS
IIT JEE PREVIOUS YEAR|Exercise TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)|1 Videos
Similar Questions
Explore conceptually related problems
IIT JEE PREVIOUS YEAR-CIRCLE-Topic 5 Analytical & Descriptive Questions
- Let 2x^2 +y^2-3xy = 0 be the equation of a pair of tangents drawn from...
Text Solution
|
- Let T1, T2 and be two tangents drawn from (-2, 0) onto the circle C:x^...
Text Solution
|
- C(1) and C(2) are two concentrate circles, the radius of C(2) being t...
Text Solution
|
- Find the intervals of the values of a for which the line y+x=0 bisects...
Text Solution
|
- Let a circle be given by 2x(x-1)+y(2y-b)=0,(a!=0,b!=0) . Find the cond...
Text Solution
|
- Lines 5x + 12y - 10 = 0 and 5x - 12y - 40 = 0 touch a circle C1 of dia...
Text Solution
|
- Through a fixed point (h, k) secants are drawn to the circle x^2 +y^2 ...
Text Solution
|
- . Let A be the centre of the circle x^2+y^2-2x-4y-20=0 Suppose that th...
Text Solution
|