A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
MTG GUIDE|Exercise NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)|19 VideosGRAVITATION
MTG GUIDE|Exercise NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)|6 VideosGRAVITATION
MTG GUIDE|Exercise NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)|9 VideosBEHAVIOUR OF PERFECT GAS AND KINETIC THEORY
MTG GUIDE|Exercise AIPMT / NEET (MCQs)|11 VideosKINEMATICS
MTG GUIDE|Exercise AIPMT/ NEET MCQs|31 Videos
Similar Questions
Explore conceptually related problems
MTG GUIDE-GRAVITATION-NEET CAFE TOPICWISE PRACTICE QUESTIONS (UNIVERSAL LAW OF GRAVITATION)
- The universal law of gravitational is the force law known also as the
Text Solution
|
- Two identical spheres of radius R made of the same material are kept a...
Text Solution
|
- Three equal masses of 1 kg each are placed at the vertices of an equil...
Text Solution
|
- Suppose the gravitational force varies inversely as the nth power of d...
Text Solution
|
- Mass M is split into two parts m and (M-m), which are then separated b...
Text Solution
|
- Three indentical bodes of mass M are locatd at the verticles of a...
Text Solution
|
- A uniform ring of mass M and radius R is placed directly above a unifo...
Text Solution
|
- Two solid spherical planets of equal radii R having masses 4M and 9M t...
Text Solution
|
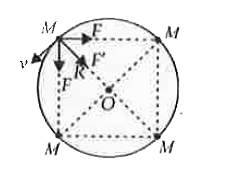
- Four particles, each of mass M and equidistant from each other, move a...
Text Solution
|
- If two particles each of mass m are placed at the two vertices of an e...
Text Solution
|
- A point mass m is placed inside a spherical shell of radius R and mass...
Text Solution
|
- The magnitudes of the gravitational field at distance r(1) and r(2) fr...
Text Solution
|
- Two point masses A and B having masses in the ratio 4:3 are separated ...
Text Solution
|
- A planet of radius R=(1)/(10)xx(radius of Earth) has the same mass den...
Text Solution
|
- The gravitational force of attraction between a uniform sphere of mass...
Text Solution
|