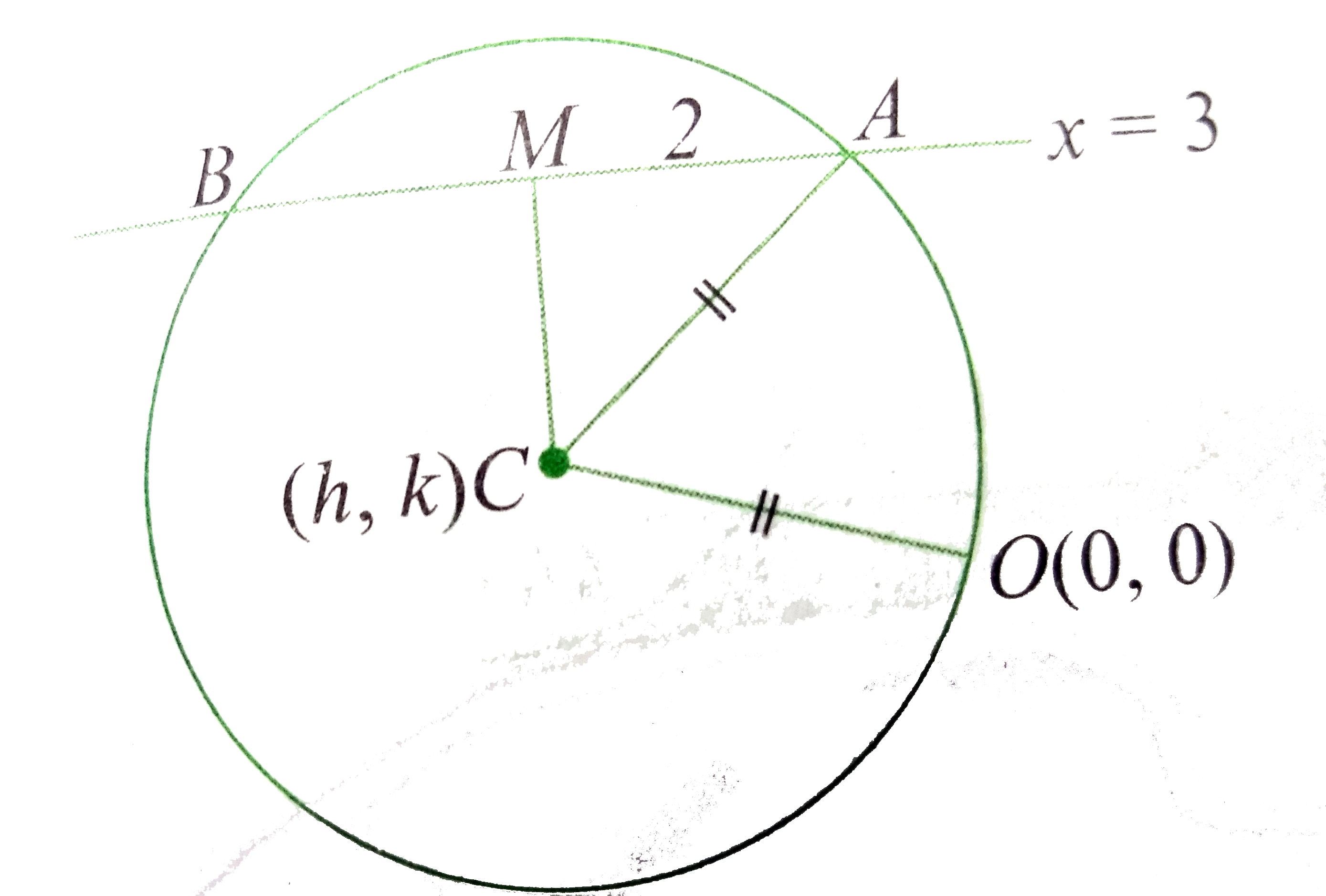Home
Class 12
MATHS
The locus of centre of a circle which pa...

The locus of centre of a circle which passes through the origin and cuts off a length of 4 units on the line `x =3` is

Text Solution

Verified by Experts

The correct Answer is:
`y^(2)+6x=13`

From the figure,
`CO=CA`
or `CO^(2)=CM^(2)+AM^(2)`
`implies (h-0)^(2)+(k-0)^(2)=((|h-3|)/(1))^(2)+4`
`impliesh^(2)+k^(2)=h^(2)-6h+13`
or `k^(2)= -6h+13`
or `k^(2)+h=13`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.7|5 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.8|5 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.5|5 Videos

  • BINOMIAL THEOREM

    CENGAGE ENGLISH|Exercise Matrix|4 Videos

  • CIRCLES

    CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Find the locus of the centre of a circle which passes through the origin and cuts off a length 2b from the line x=c .

Find the locus of the centre of a circle which passes through the origin and cuts off a length 2l from the line x=c .

Find the equation of the circle which passes through the origin and cut off equal chords of sqrt(2) units from the lines y=xa n dy=-xdot

The locus of the centres of all circles passing through two fixed points.

Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the circle concentric with the circle x^2+y^2-6x+12 y+15=0\ and double of its area.

Find the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=x and y=-x

Find the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.

Equation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is

Find the equation of a circle which passes through the origin and whose centre is (a, b).

The equation of the circles which pass through the origin and makes intercepts of lengths 4 and 8 on the x and y-axis respectively are