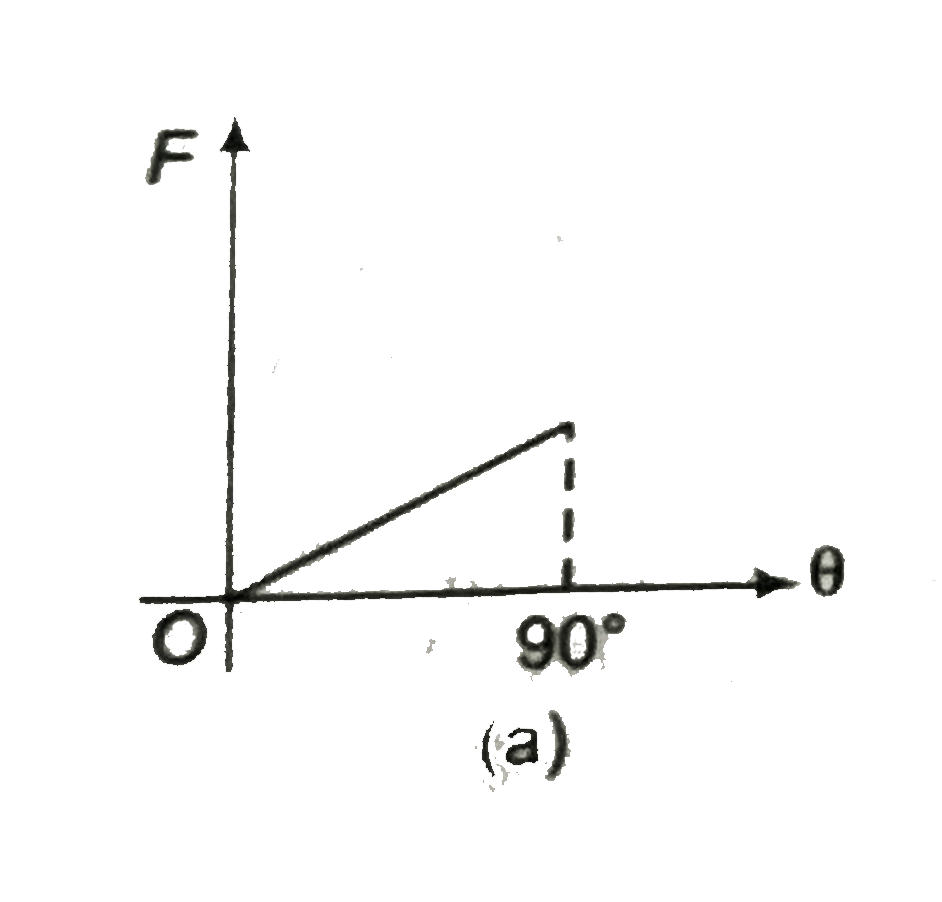
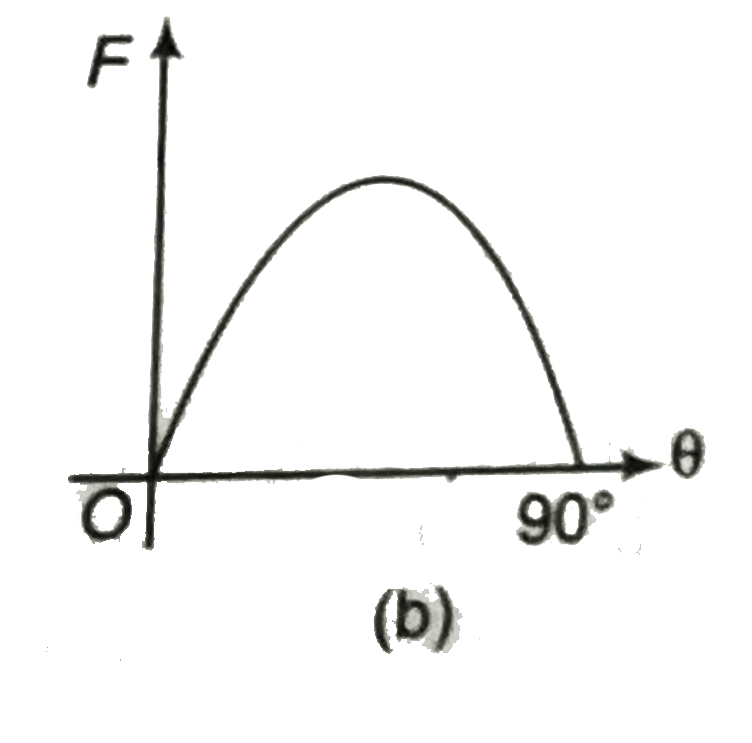
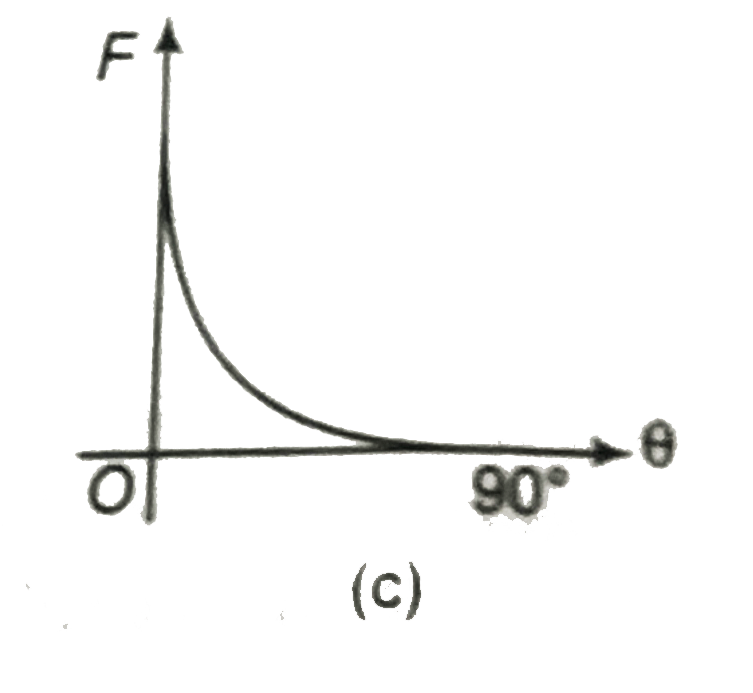
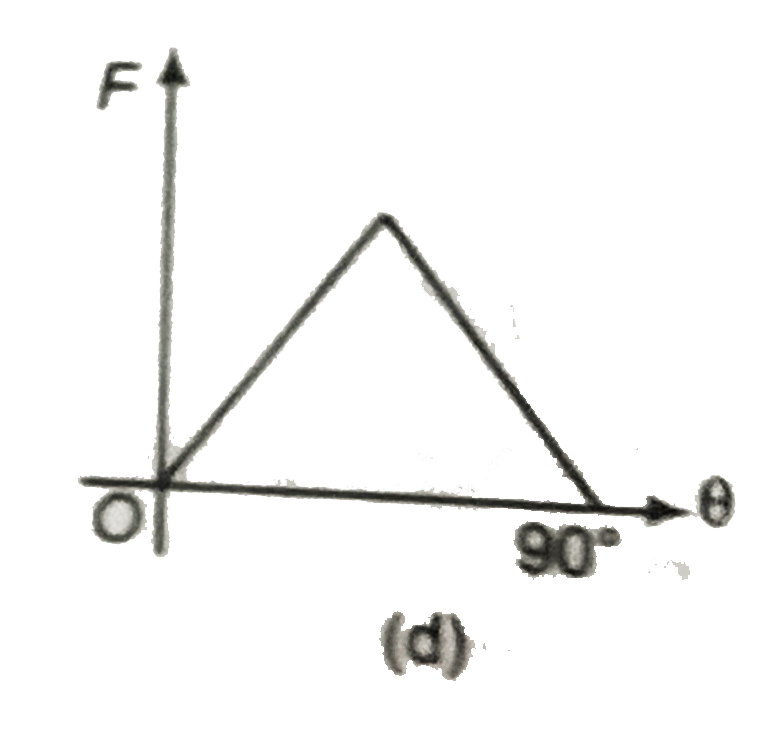
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
LAWS OF MOTION
DC PANDEY ENGLISH|Exercise Objective Question|32 VideosLAWS OF MOTION
DC PANDEY ENGLISH|Exercise Comprehension|9 VideosLAWS OF MOTION
DC PANDEY ENGLISH|Exercise Assertion And Reason|28 VideosKINEMATICS 1
DC PANDEY ENGLISH|Exercise INTEGER_TYPE|15 VideosLAWS OF THERMODYNAMICS
DC PANDEY ENGLISH|Exercise Level 2 Subjective|18 Videos
DC PANDEY ENGLISH-LAWS OF MOTION-Single Correct
- In the figure shown find relation between magnitudes of a(A) and a(B).
Text Solution
|
- In the figure block moves downwards with velocity v(1), the wedge righ...
Text Solution
|
- In the figure the minimum value of a at which the cylinder starts risi...
Text Solution
|
- When the trolley show in figure is given a horizontal acceleration a, ...
Text Solution
|
- In the arrangement shown in the figure the mass M is very heavy compar...
Text Solution
|
- A block rests on a rough plane whose inclination theta to the horizont...
Text Solution
|
- The minimum value of mu between the two blocks for no slipping is
Text Solution
|
- A block is sliding along an inclined plane as shown in figure . If the...
Text Solution
|
- In the figure the wedge is pushed with an acceleration of sqrt3 m//s ^...
Text Solution
|
- Two block A and B are separted by some distance and tied by a string a...
Text Solution
|
- All the surface and pulleys are frictionless in the shown arrangement....
Text Solution
|
- Two blocks of 2 kg and 4 kg are connected by a light string and kept o...
Text Solution
|
- A smooth rod length l is kept inside a trolley at an angle theta as sh...
Text Solution
|
- A car begains from rest at time t = 0, and then acceleration along a s...
Text Solution
|
- A horizontal plank is 10.0 m long with uniform density and mass 10 kg ...
Text Solution
|
- A block is kept on a smooth inclined plane of angle of inclination the...
Text Solution
|
- A uniform cube of mass m and slidea is resting in equilibrium on a rou...
Text Solution
|
- A horizontal force F = (mg)/(3) is applied on the upper surface of a u...
Text Solution
|
- Two persons of equal heights are carrying a long uniform wooden plank ...
Text Solution
|
- A ball connect ed with string is released at an angle 45^(@) with the ...
Text Solution
|