Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.1|15 VideosKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.2|25 VideosKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise Integer|9 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 VideosKINETIC THEORY OF GASES
CENGAGE PHYSICS ENGLISH|Exercise Compression|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Solved Examples
- Two towers AB and CD are situated at a distance d apart, as shown in ...
Text Solution
|
- Two particle are projected with same initial velocities at an angle 30...
Text Solution
|
- A large , heavy box is sliding without friction down a smooth plane o...
Text Solution
|
- Find the point on the curve y^2=a x the tangent at which makes an angl...
Text Solution
|
- An aircraft is .flying. horizontally with a constant vefocity =200m//s...
Text Solution
|
- The speed of a boat in still water is 15 km/hr. It can go 30 km ups...
Text Solution
|
- Three particles A, B and C are situated at the vertices of an equilate...
Text Solution
|
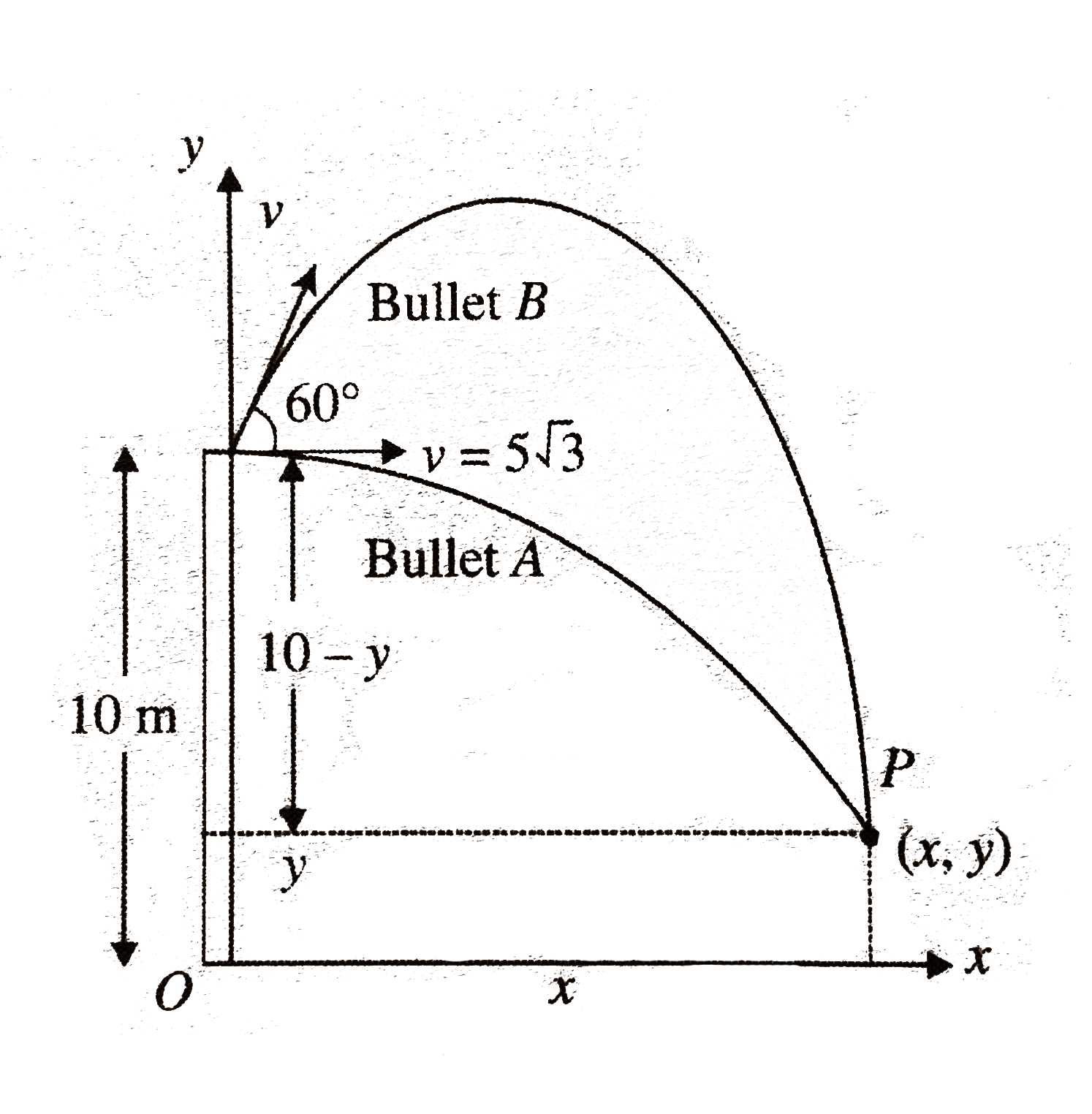 ,
, .
.