Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise Subjective|40 VideosKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise Single Correct|76 VideosKINEMATICS-2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 5.3|12 VideosKINEMATICS-1
CENGAGE PHYSICS ENGLISH|Exercise Integer|9 VideosKINETIC THEORY OF GASES
CENGAGE PHYSICS ENGLISH|Exercise Compression|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-KINEMATICS-2-Exercise 5.4
- Particles A and B move with constant and equal speeds in a circle as s...
Text Solution
|
- Particles A and B move with constant and equal speeds in a circle as s...
Text Solution
|
- Find the angular velocity of A with respect to O at the instant shown ...
Text Solution
|
- A particle travels in a circle of radius 20 cm at a speed thast unifor...
Text Solution
|
- Find the magnitude of the linear acceleration of a particle moving in ...
Text Solution
|
- A particle in a circular path speeds up with a uniform rate between tw...
Text Solution
|
- The linear speed of a particle moving in a circle of radius R varies w...
Text Solution
|
- A particle at the edge of a ratating disc speeds up at a uniform angul...
Text Solution
|
- The angular velocity of a particle moving in a circle realative to the...
Text Solution
|
- Two particles 1 and 2 move with velocities vec v1 and vec v2 making th...
Text Solution
|
- Two satellities 1 and 2 orbiting with the time periods T1 and T2, resp...
Text Solution
|
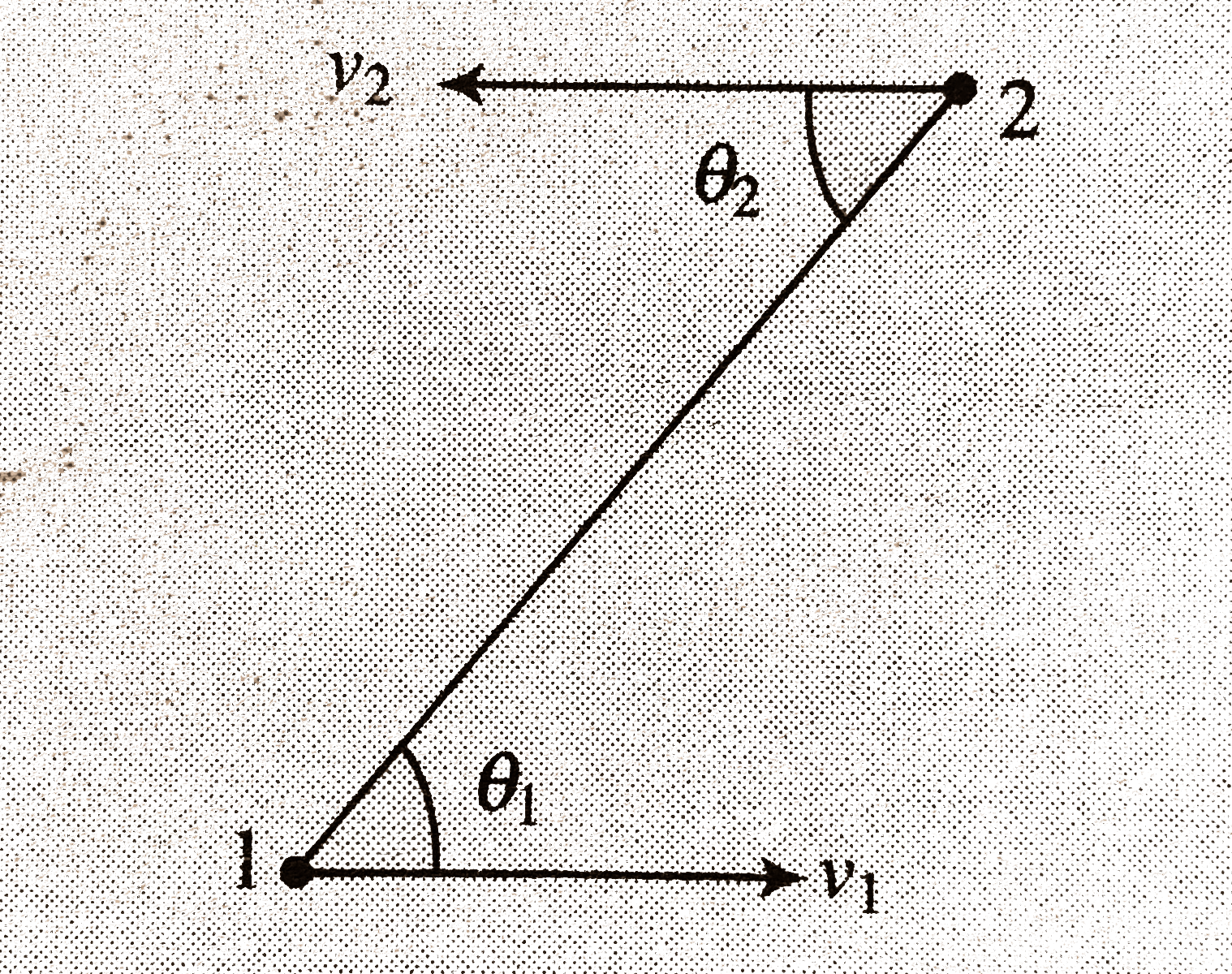 .
.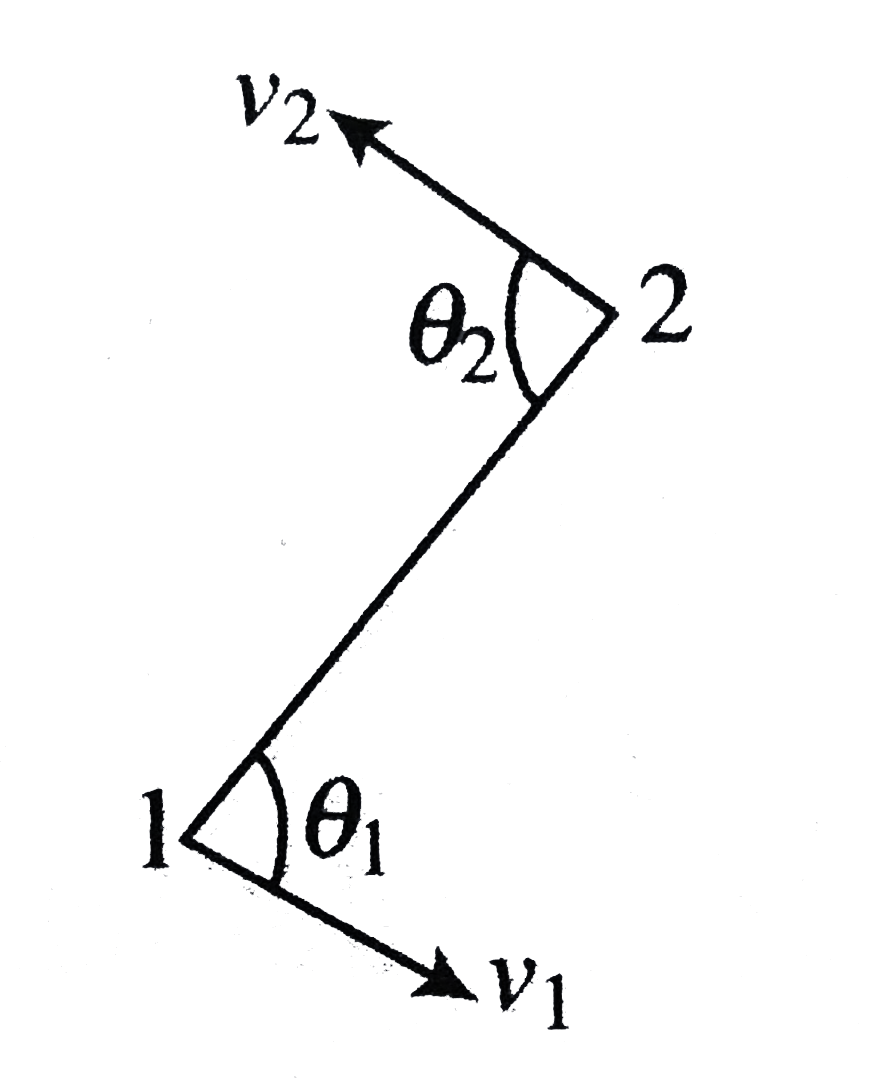 ,
, .
.