Given the setup shown in Fig Block `A, B` and `C` have masses `m_(A)= M` and `m_(B) =m_(C) = m`. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block `B` and the support table, but there is friction between blocks `B` and `C`, denoted by a given coefficient `mu`

a . In terms the given find (i) the acceleration of block `A` and `B`
b. Suppose the system is released from rest with block `C` near the right end of block `B` as shown in the above figure. If the the length `L` of block `B` is given, what is the speed of block `C` as it reached the left end of block `B` ? Tear the size of `C` as small
c. If the mass of block `A` is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.

Explanation

a. Apply constrain on string , the length of strings is constant . Differentiate twice to get relation between acceleration .Let the acceleration of block `A,B` and `C` be a, b and c respectively

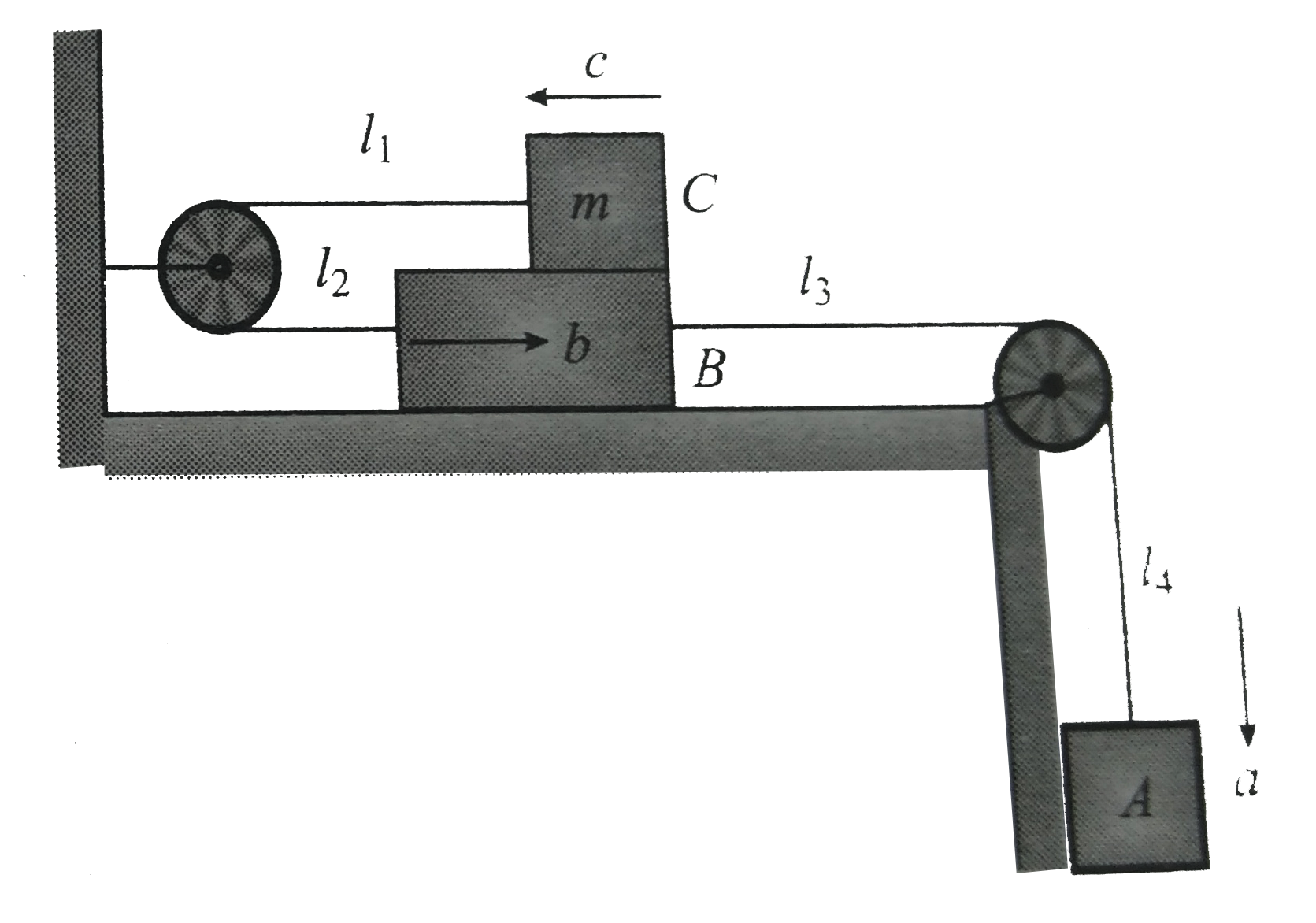
`l_(1) + l_(2) =` constant
`l_(3) + l_(4) =` constant
`overset(..)l_(1) + overset(..)l_(2) = 0 rArr |b| = |c|`
`overset(..)l_(3) + overset(..)l_(4) = 0 rArr |a| = |b|`
From which we get `a = b = c`
From `FBD` of `A , B` and `C` [Fig (a)]

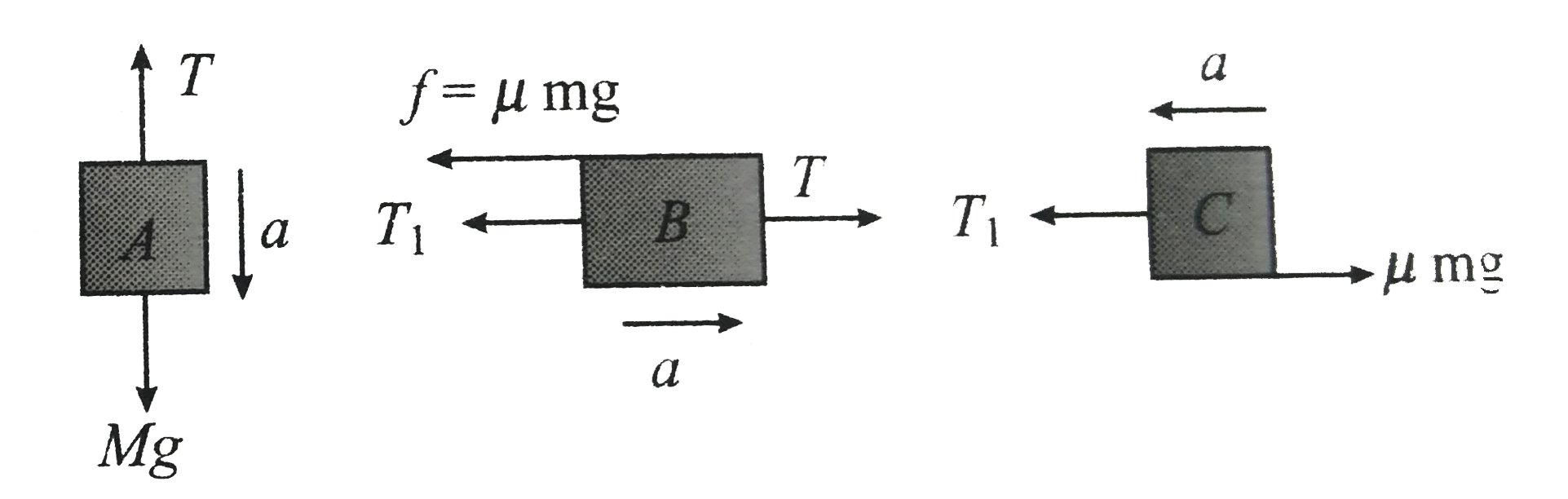
Writing equation of motion for block `A` :
` Mg - T = Ma` .....(i)
For block `B , T - T_(1) - mu mg = ma` .....(ii)
Solving equation (i) ,(ii) and (iii) we get
`a = ((M - 2 mu m )/(M + 2m))g`....(iv)
Putting a in Eq (i), we get
`Mg - T = M ((M - 2 mu m )/(M + 2m))g rArr T = (2m Mg (1 + mu))/((M + 2m))`
b. As there is relative motion between blocks , we apply
`v_(rel)^(2) = v_(rel)^(2) + 2a_(rel) S_(rel)`
If system is released from rest `u_(rel) = 0`
`v_(rel)^(2)= 2a_(rel) S_(rel) rArr v_(rel)= sqrt(2a_(rel) S_(rel))`
`a_(rel) = 2a` and `S_(rel) = L`
`rArr v = sqrt((4gL(M - 2 mu m))/((M + 2m)))`
cIf blocks will not acceleration , than put `a = 0 `in Eq (iv) to get`M = 2mu m`.