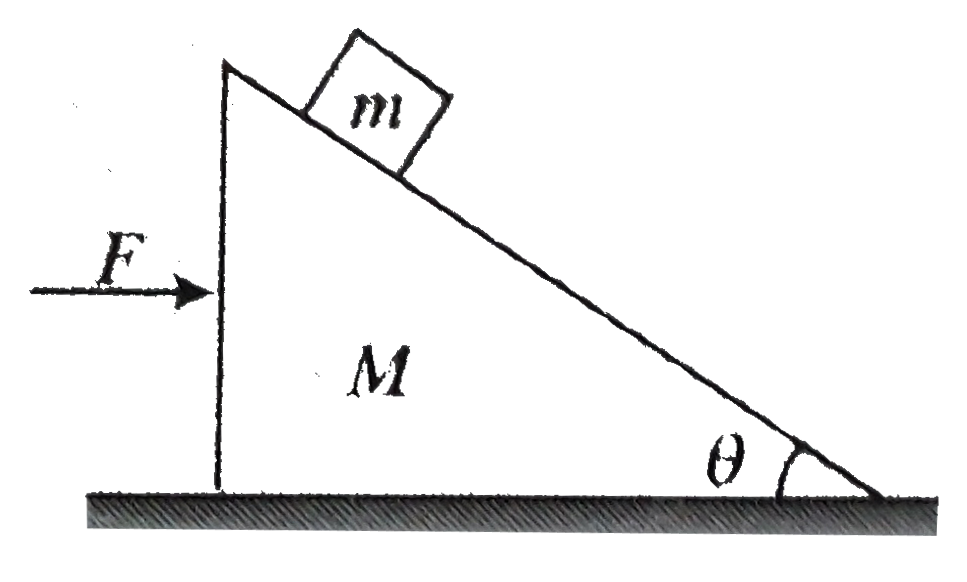
Here if both the masses are moving together , accceleration of the system will be `a = F1 (M + m)` .If we observe the mass `m` relation to `M` . It experience a pseudo force out `ma` toward left . Along the incline it experience two forces `mg sin theta` downwards and `ma cos theta ` upward . If `mg sin theta `is morethen `ma cos theta `will act in upward direction here if block `m` is in equlibrium on inclined surface , we most have
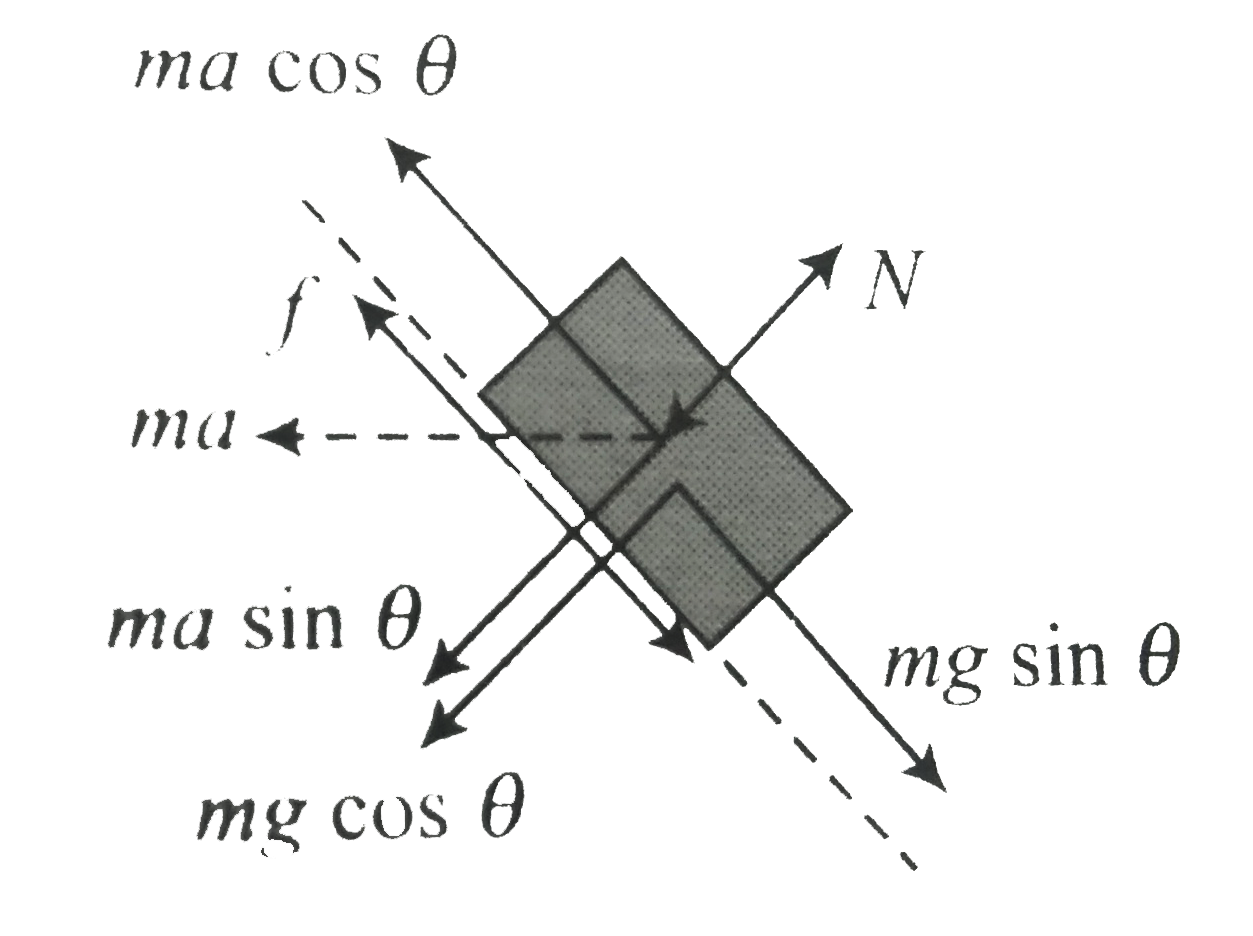
`f = mu N`,
Here `f = (mg sin theta - ma cos theta)`
and `N = (ma sin theta + mg cos theta)`
`f = mg sin theta - ma cos theta le mu (mg cos theta +ma sin theta)`
or `a ge (sin theta - mu cos theta )/(cos theta + mu sin theta )g`
or `(M + m) a ge (sin theta - mu cos theta )/(cos theta + mu sin theta )(M + m)g`
`F ge (sin theta - mu cos theta )/(cos theta + mu sin theta )(M + m)g`....(i)
If force is more than the value obtaional in Eq (i) `ma cos theta ` will increase on `m` and the static friction on it will derection At `a = g tan theta` (when `F = (M + m)g tan theta )` we know that the force `mg sin theta` will be balanced by `ma cos theta` at this acceleration no friction will act on it , if applied force will increase belond values , `ma cos theta ` will execed `mg sin theta ` and friction static in downward direction here if block `m` is in equation we must have `f = (ma cos theta - mg sin theta )N = (mg cos theta + ma sin theta )` and `f le mu N`
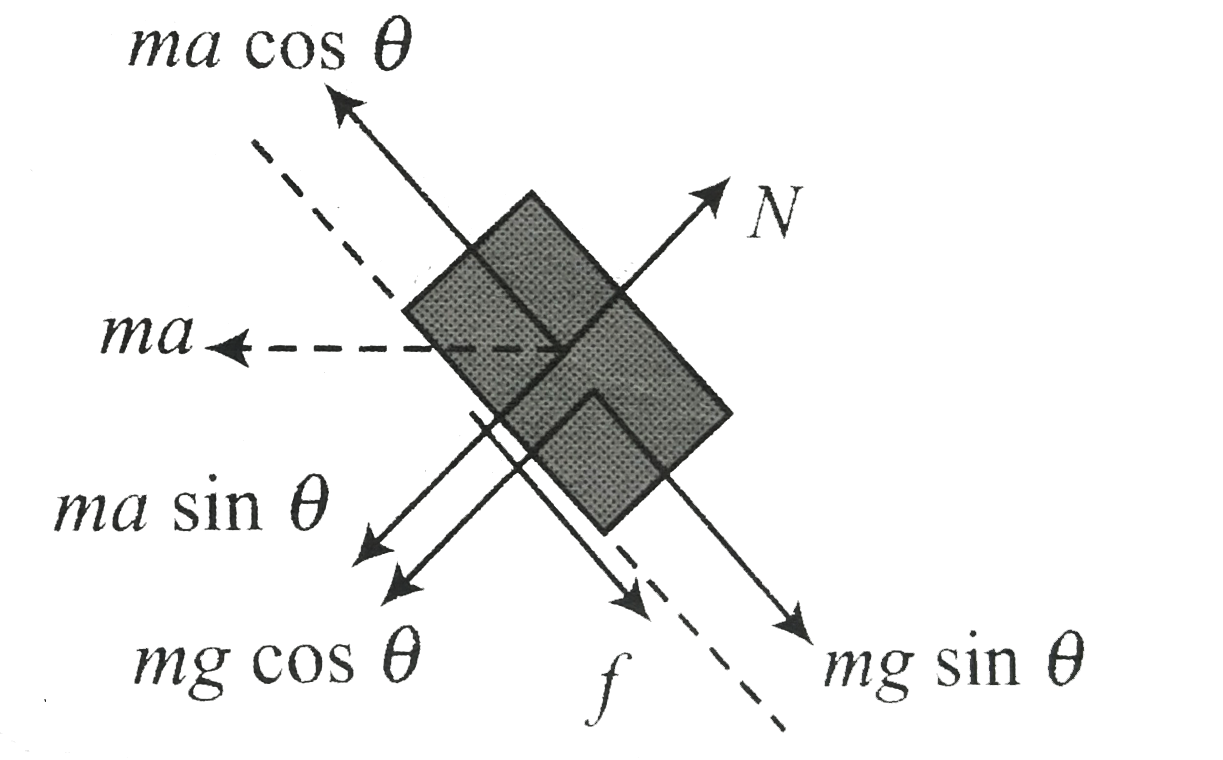
`ma cos theta - mg sin theta le mu(mg cos theta + ma sin theta )`
`rArr a le (sin theta + mu cos theta )/(cos theta - mu sin theta )g`
`rArr (M + m) a le (sin theta + mu cos theta )/(cos theta - mu sin theta) (M + m)g`
` rArr F le (sin theta + mu cos theta )/(cos theta - mu sin theta) (M + m)g`
Hence `F_(min) le (sin theta - mu cos theta )/(cos theta + mu sin theta) (M + m)g`
and `F_(max) le (sin theta + mu cos theta )/(cos theta - mu sin theta) (M + m)g`