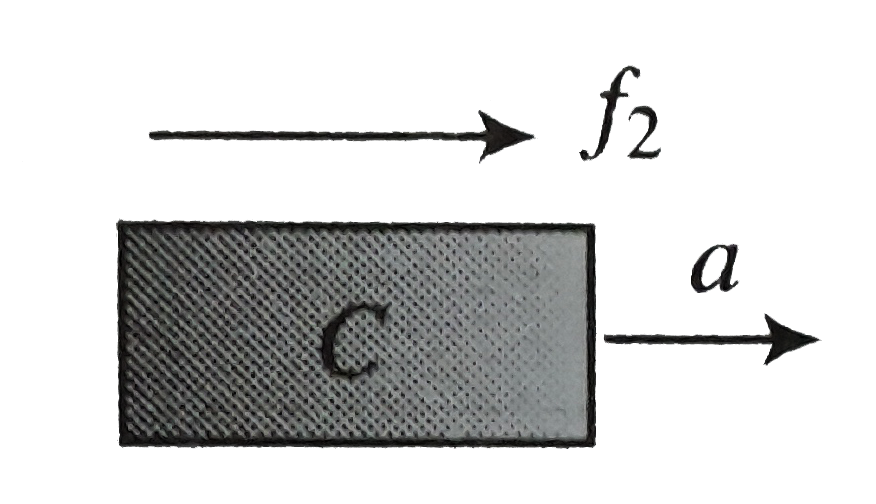
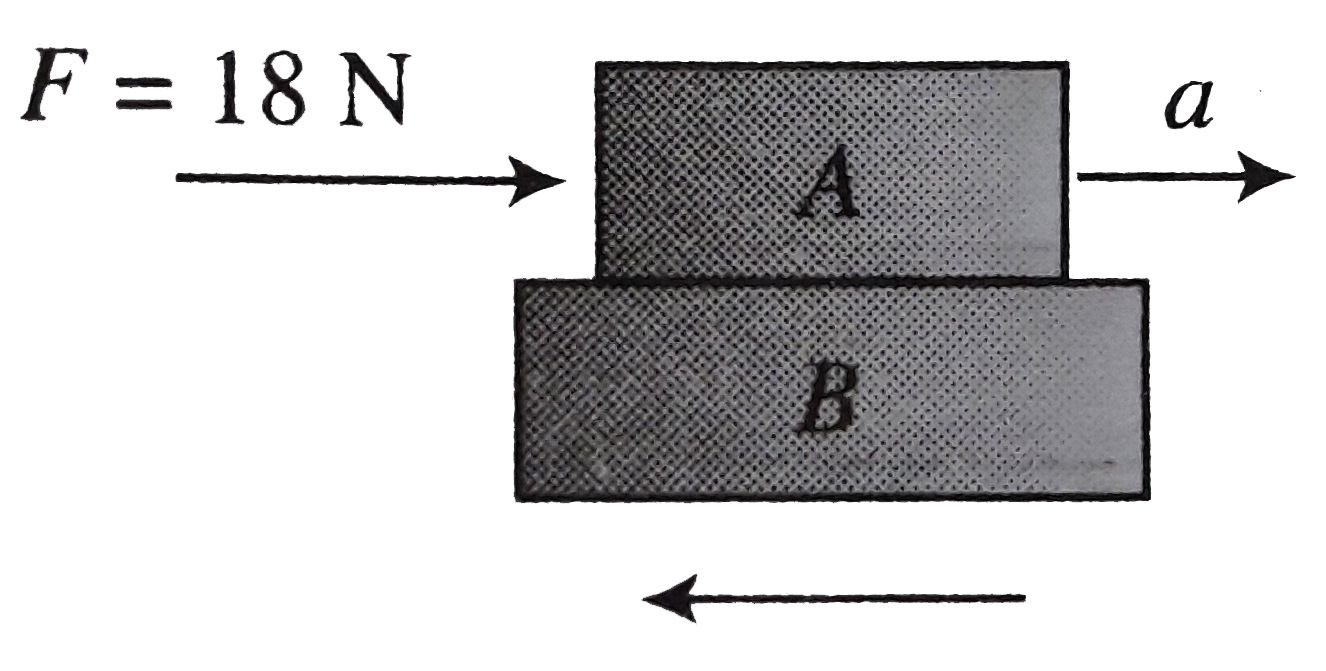
Text Solution
Verified by Experts
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 7.1|25 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS ENGLISH|Exercise Exercise 7.2|16 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS ENGLISH|Exercise Integer type|1 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|5 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-NEWTON'S LAWS OF MOTION 2-Solved Examples
- In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively...
Text Solution
|
- Blocks A, B and C are placed as shown in Fig and connected by the rops...
Text Solution
|
- Two blocks A and B of equal masses are placed on rough inclined plane ...
Text Solution
|
- Find the acceleration a(1) , a(2) and a(3) of the three blocks shown i...
Text Solution
|
- In the sitution shown in figure there is no friction between 2 kg and...
Text Solution
|
- Consider three blocks placed one over the other as shown in Fig. Let a...
Text Solution
|
- A track consists of two circular pars ABC andCDE of equal rdius 100 m ...
Text Solution
|
- Two blocks A(m(A) = 5 kg) and B(m(B)= 15 kg) are placed as shown in Fi...
Text Solution
|
- A block of mass m(1) = 20 kg as placed on a wedge of mass m(2)= 30 kg ...
Text Solution
|
- Consider the situation shown in Fig. The hirizontal surface below the ...
Text Solution
|
- A metal ring of mass m and radius R is placed on a smooth horizontal t...
Text Solution
|
- A thin uniform copper rod of length l and mass m rotates uniformly wit...
Text Solution
|