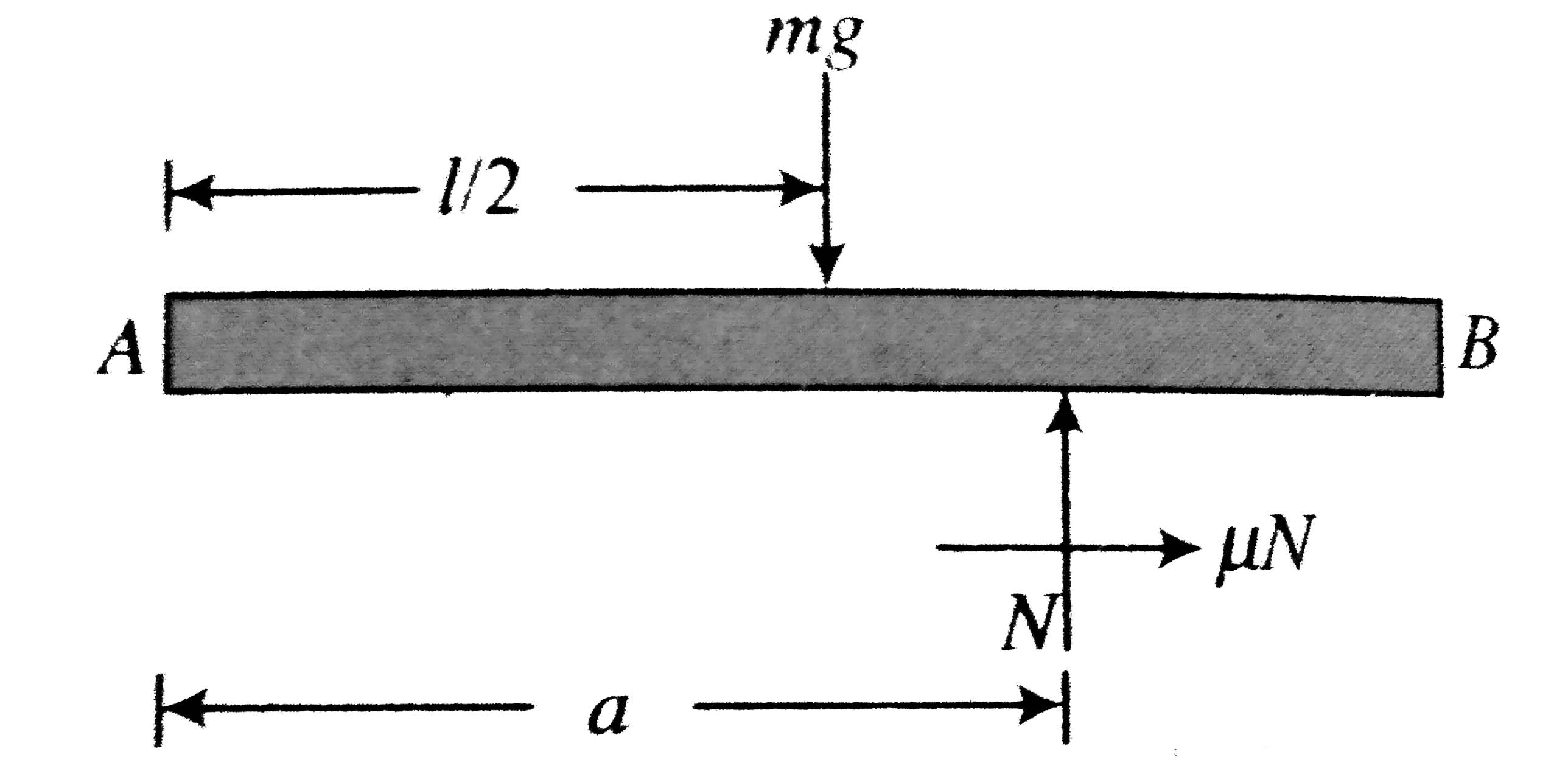
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Single Correct|97 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Multiple Correct|9 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Exercise 2.4|11 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|2 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS ENGLISH|Exercise Interger|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Subjective
- In the instant shown in the diagram the board is moving up (vertically...
Text Solution
|
- A weightless rod of length l with a small load of mass m at the end is...
Text Solution
|
- A cylinder of weight W and radius R is to be raised onto a horizontal...
Text Solution
|
- A cylinder is rolling without sliding over two horizontal planks (surf...
Text Solution
|
- A block of mass M= 4 kg of height and breath b is placed on a rough pl...
Text Solution
|
- A uniform rod AB of mass m and length l is suspended by two massless a...
Text Solution
|
- A cylinder rests on a horizontal rotating disc, as shown in the figure...
Text Solution
|
- A uniform slender bar AB of mass m is suspended as shown from a small ...
Text Solution
|
- A uniform bar of length I and mass m stands vertically touching a vert...
Text Solution
|
- A uniform cube of side 'a' and mass m rests on a rough horizontal tabl...
Text Solution
|
- Find minimum value of l so that truck can avoid the dead end, without ...
Text Solution
|
- A uniform rod of mass m and length l can rotate in vertical plane abou...
Text Solution
|
- A wheel of radius R=10 cm and moment of inertia I=0.05kg m^(2) is rota...
Text Solution
|