A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
PROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise LC_TYPE|3 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise INTEGER_TYPE|2 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS ENGLISH|Exercise Fill In The Blanks|1 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS ENGLISH|Exercise Integer type|1 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS ENGLISH|Exercise Integer|11 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS ENGLISH-PROPERTIES OF SOLIDS AND FLUIDS-SCQ_TYPE
- The following four wires of length L and radius r are made of the same...
Text Solution
|
- Two rods of different materials having coefficients of linear expansio...
Text Solution
|
- The adjacent graph shows the extension(Deltal) of a wire of length 1 m...
Text Solution
|
- When temperature of a gas is 20^@C and pressure is changed from p(1)= ...
Text Solution
|
- A glass tube of uniform internal radius(r) has a valve separating the ...
Text Solution
|
- Â One end of a horizontal thick copper wire of length 2L and radius ...
Text Solution
|
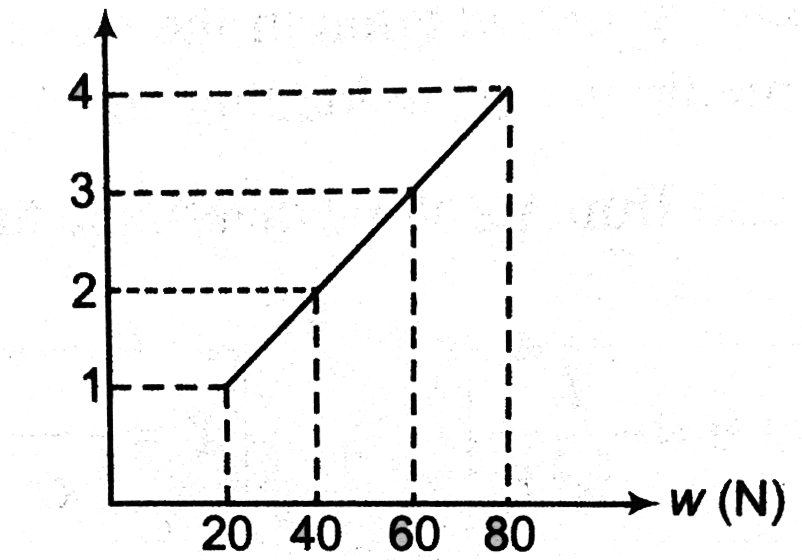 .
.