Home
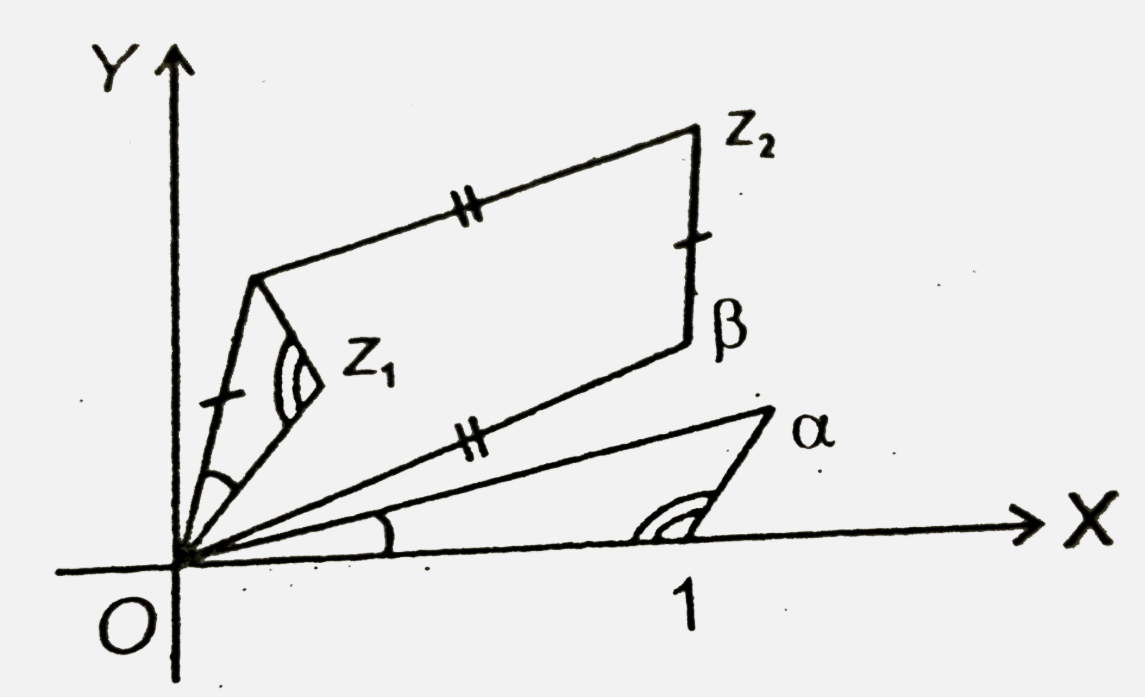
Class 12
MATHS
Let z(1), alpha, beta be complex numbe...

Let ` z_(1), alpha, beta ` be complex numbers of which ` alpha and beta` constants and ` z_(1)` varies. If ` z_(2)` is given in terms of ` z_(1) ` by one of the following equations, it is required to find `z_(2)` corresponding to ` z_(1)` then
In the given figure

A

`z_(2) = alphaz_(1) +beta`

B

`z_(2) = (alphaz_(1))/beta`

C

`z_(2)=alpha beta z_(1)`

D

`z_(2) = beta z_(1)`

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • COMPLEX NUMBERS AND QUADRATIC EQUATIONS

    AAKASH INSTITUTE ENGLISH|Exercise Assertion -Reason Type Questions|19 Videos

  • COMPLEX NUMBERS AND QUADRATIC EQUATIONS

    AAKASH INSTITUTE ENGLISH|Exercise Section-F ( Matrix -Match type Question)|7 Videos

  • COMPLEX NUMBERS AND QUADRATIC EQUATIONS

    AAKASH INSTITUTE ENGLISH|Exercise Assignment (Section -C) (objective Type Questions ( more thena one options are correct )|35 Videos

  • BINOMIAL THEOREM

    AAKASH INSTITUTE ENGLISH|Exercise Assignment (section-J) Objective type question (Aakash Challengers Questions)|4 Videos

  • CONIC SECTIONS

    AAKASH INSTITUTE ENGLISH|Exercise SECTION - J ( Aakash Challengers Questions )|16 Videos

Similar Questions

Explore conceptually related problems

Let z_(1), alpha, beta be complex numbers of which alpha and beta constants and z_(1) varies. If z_(2) is given in terms of z_(1) by one of the following equations, it is required to find z_(2) corresponding to z_(1) then The given figure illustrates

Let z_1 and z_2 q, be two complex numbers with alpha and beta as their principal arguments such that alpha+beta then principal arg(z_1z_2) is given by:

Let z_1, z_2 be two complex numbers with |z_1| = |z_2| . Prove that ((z_1 + z_2)^2)/(z_1 z_2) is real.

Let z_(1),z_(2) be two complex numbers such that z_(1)+z_(2) and z_(1)z_(2) both are real, then

Let z_1, z_2 be two complex numbers represented by points on the circle |z_1|= and and |z_2|=2 are then

If z_(1) and z_(2) are two complex numbers such that |z_(1)|= |z_(2)| , then is it necessary that z_(1) = z_(2)

z_(1) "the"z_(2) "are two complex numbers such that" |z_(1)| = |z_(2)| . "and" arg (z_(1)) + arg (z_(2) = pi," then show that "z_(1) = - barz_(2).

For complex number z,|z-1|+|z+1|=2, then z lies on

Let z_(1) and z_(2) be two given complex numbers such that z_(1)/z_(2) + z_(2)/z_(1)=1 and |z_(1)| =3 , " then " |z_(1)-z_(2)|^(2) is equal to

Let z_1a n dz_2 be two complex numbers such that ( z )_1+i( z )_2=0 and arg(z_1z_2)=pidot Then, find a r g(z_1)dot