Home
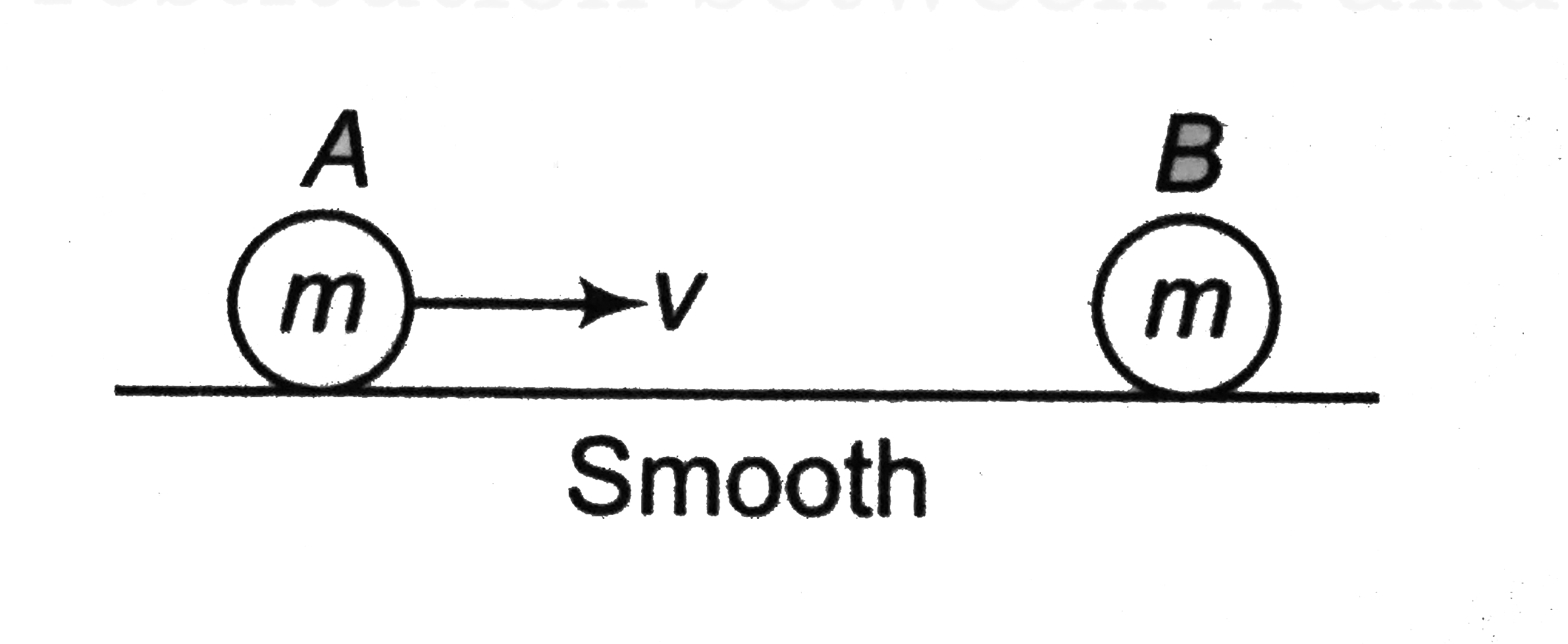
Class 12
PHYSICS
In the figure shown, coefficient of rest...

In the figure shown, coefficient of restitution between A and B is `e=1/2`, then

A

velocity of B after collision is `(v)/(2)`

B

impulse on one of the balls during collision is `(3)/(4)`mv

C

loss of kinetic energy in collision is `(3)/(16) mv^(2)`

D

loss of kinetic energy in the collision is `(1)/(4) mv^(2)`

Text Solution

Verified by Experts

The correct Answer is:
B, C

By momentum conservation in horizontal direction `V = V_(1) + V_(2)` ….(i)
and `e = (V_(2) - V_(1))/(V) = (1)/(2)` ….(ii)
By (i) and (ii) `V_(2) = (3V)/(4)`
So impulse on `B = m ((3V)/(4))`
and loss in `K.E. = (3)/(16) mV^(2)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEM

    RESONANCE ENGLISH|Exercise DPP No.64|20 Videos

  • DAILY PRACTICE PROBLEM

    RESONANCE ENGLISH|Exercise DPP No.65|9 Videos

  • DAILY PRACTICE PROBLEM

    RESONANCE ENGLISH|Exercise DPP No.62|9 Videos

  • CURRENT ELECTRICITY

    RESONANCE ENGLISH|Exercise High Level Problems (HIP)|19 Videos

  • ELECTRO MAGNETIC WAVES

    RESONANCE ENGLISH|Exercise Exercise 3|27 Videos

Similar Questions

Explore conceptually related problems

In the figure shown, the force of friction between A and B will be :

A ball of mass m collides with a stationary wedge of mass M , perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e , calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

In the figure shown, the total resistance between A and B is

Two identical balls of equal masses A and B, are lying on a smooth surface as shown in the figure. Ball A hits the ball B (which is at rest) with a velocity v=16ms^-1 . What should be the minimum value of coefficient of restitution e between A and B so that B just reaches the highest point of inclined plane? (g=10ms^-2)

A ball strickes a horizontal floor at an angle theta = 45^@ with the normal to floor. The coefficient of restitution between the ball and the floor is e = 1//2 . The fraction of its kinetic energy lost in the collision is.

A ball strickes a horizontal floor at an angle theta = 45^@ with the normal to floor. The coefficient of restitution between the ball and the floor is e = 1//2 . The fraction of its kinetic energy lost in the collision is.

Two blocks A and B are lying on the table as shown in the figure. The coefficient of friciton between block A and block B is mu . The coefficient of friction between block B and ground also mu . An external force F is applied in the direction shown. The maximum value of the force F that can be applied without moving the blocks.

A ball stikes a horizontal floor at an angle theta = 30° with normal to the floor . The coefficient of restitution between the ball and floor is. e = 1/3 . The percentage of its kinetic energy lost in the collision is nearly

In the figure shown the equivalent capacitance between 'A' and 'B' is :

A ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1//2 , is