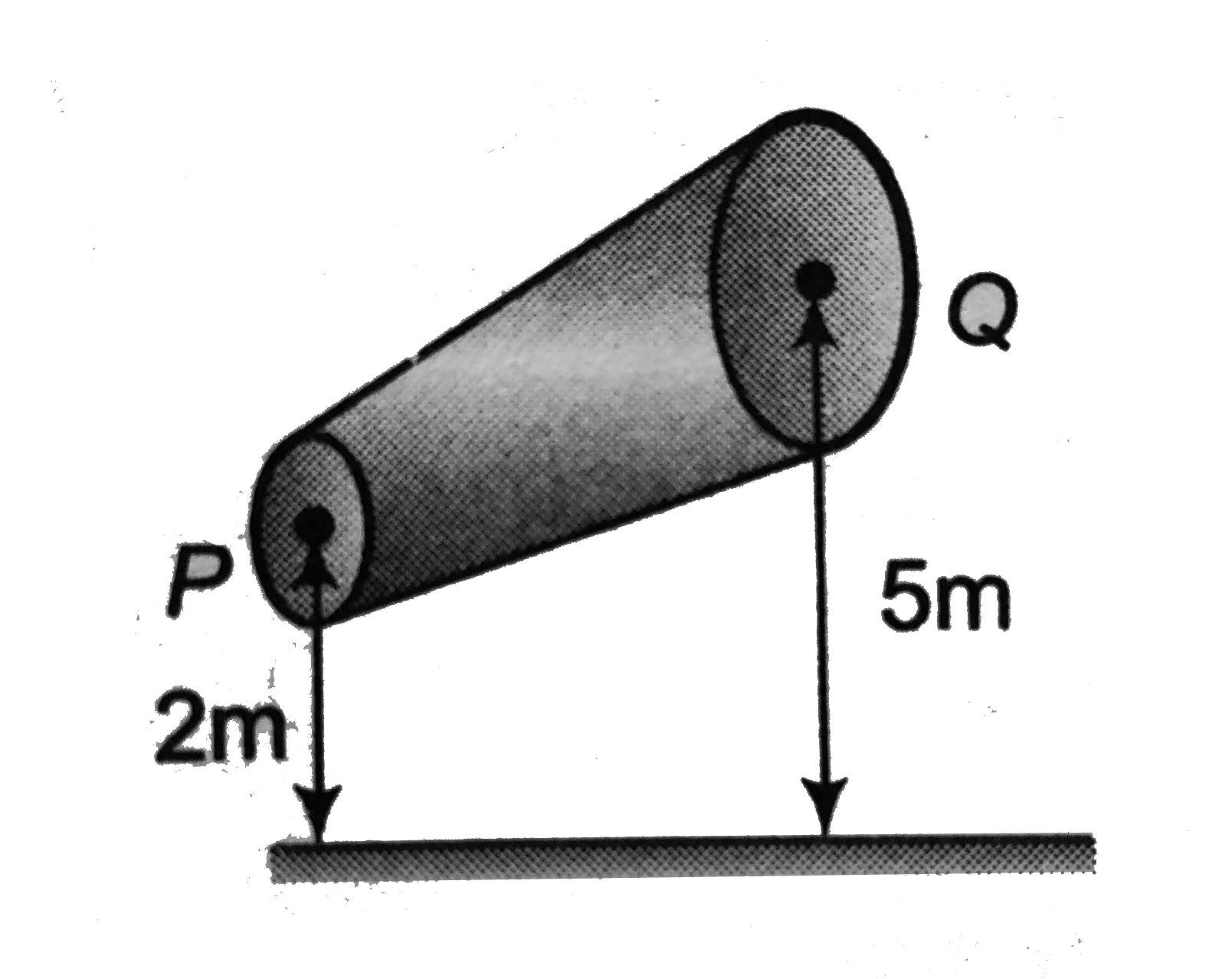
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
FLUID MECHANICS
RESONANCE ENGLISH|Exercise Exercise- 2 PART - III|7 VideosFLUID MECHANICS
RESONANCE ENGLISH|Exercise Exercise- 2 PART - IV|5 VideosFLUID MECHANICS
RESONANCE ENGLISH|Exercise Exercise- 2 PART - I|18 VideosELECTROSTATICS
RESONANCE ENGLISH|Exercise Exercise|52 VideosFULL TEST 1
RESONANCE ENGLISH|Exercise Exercise|30 Videos
Similar Questions
Explore conceptually related problems
RESONANCE ENGLISH-FLUID MECHANICS-Exercise- 2 PART - II
- A closed tube in the form of an equilateral triangle of side l contain...
Text Solution
|
- An open tank 10 m long and 2 m deep is filled up to 1.5 m height of oi...
Text Solution
|
- Figure shows a cubical block of side 10 cm and relative density 1.5 su...
Text Solution
|
- A tank containing gasoline is sealed and the gasoline is under pressur...
Text Solution
|
- A large open top container of negligible mass and uniform cross sectio...
Text Solution
|
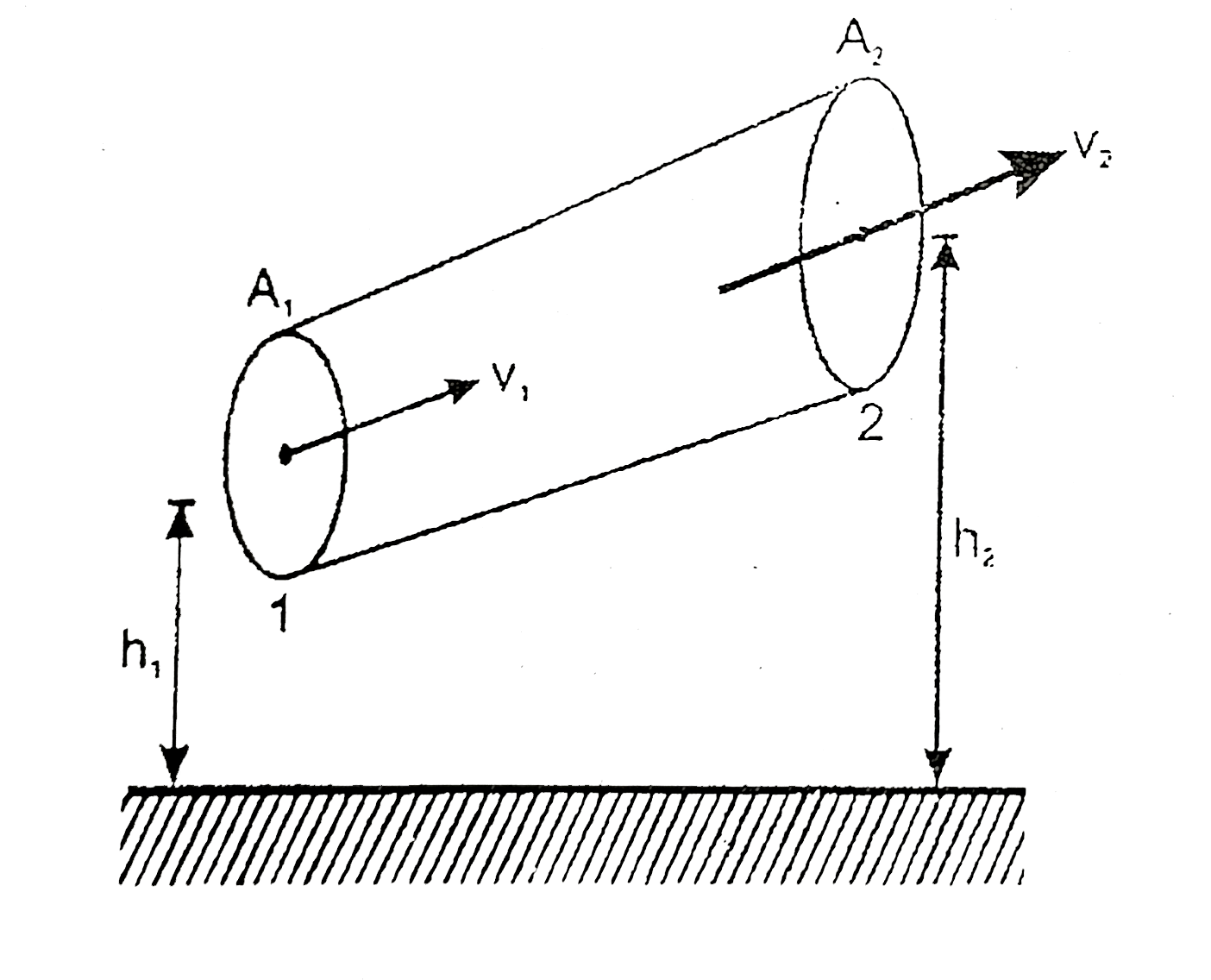
- A non-viscous liquid of constant density 1000 kg//m^(3) flows in a str...
Text Solution
|