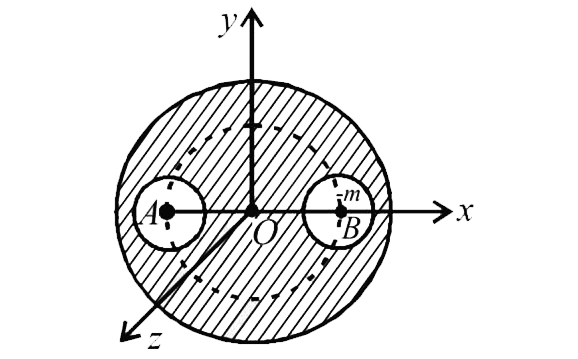
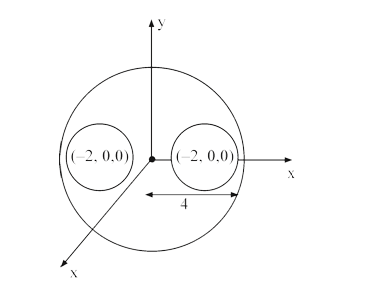
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive)ASSERTIOIN AND REASON|1 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive)MATCH MATRIX|1 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) SINGLE OPTION CORRECT|14 VideosGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE )|111 VideosINTRODUCTION TO VECTORS & FORCES
VMC MODULES ENGLISH|Exercise JEE Advanced ( ARCHIVE LEVEL-2)|12 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- The magnitude of the gravitational field at distance r1 and r2 from th...
Text Solution
|
- Two spherical planets P and Q have the same uniform density rho, masse...
Text Solution
|
- Two bodies, each of mass M, are kept fixed with a separation 2L. A par...
Text Solution
|
- A spherical body of radius R consists of a fluid of constant density a...
Text Solution
|