A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
KINEMATICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise JEE Advanced (archive)|14 VideosKINEMATICS OF A PARTICLE
VMC MODULES ENGLISH|Exercise LEVEL 2|65 VideosJEE MAIN REVISON TEST-23
VMC MODULES ENGLISH|Exercise PHYSICS (SECTION 2)|1 VideosLAWS OF MOTION
VMC MODULES ENGLISH|Exercise IMPECCABLE|53 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-KINEMATICS OF A PARTICLE -JEE MAIN (archive)
- Two balls A and B of same masses are thrown from the top of the buildi...
Text Solution
|
- Speeds of two identical cars are u and 4u at at specific instant. The ...
Text Solution
|
- A bullet fired into a fixed target loses half of its velocity after pe...
Text Solution
|
- A car moving with a speed of 50 km h^(-1) can be stopped by brakes aft...
Text Solution
|
- A particle moves in a straight line with retardation proportional to i...
Text Solution
|
- A ball is released from the top of a tower of height h metre. It takes...
Text Solution
|
- An automobile travelling with a speed 60 km//h , can brake to stop wi...
Text Solution
|
- A car, starting from rest, accelerates at the rate (f) through a dista...
Text Solution
|
- The relation between time t and distance x is t = ax^(2)+ bx where a a...
Text Solution
|
- A parachutist, after bailing out, falls 50 m without friction, When th...
Text Solution
|
- A particle located at x = 0 at time t = 0, starts moving along the pos...
Text Solution
|
- The velocity of particle is v=v(0)+"gt"+ft^(2). If its position is x=0...
Text Solution
|
- A body is at rest at x = 0. At t = 0, it starts moving in the positive...
Text Solution
|
- Consider a rubber ball freely falling from a height h = 4.9 m onto a h...
Text Solution
|
- An object , moving with a speed of 6.25 m//s , is decelerated at a ra...
Text Solution
|
- From a tower of height H, a particle is thrown vertically upwards with...
Text Solution
|
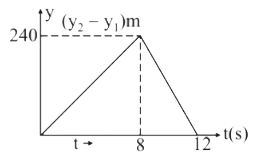
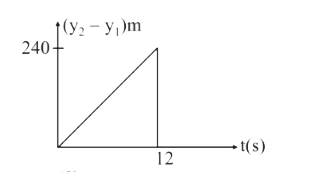
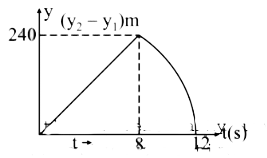
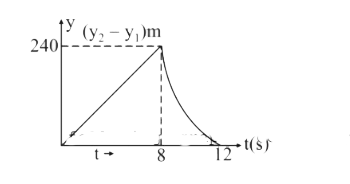
- Two stones are through up simultaneously from the edge of a cliff 240 ...
Text Solution
|
- A ball is thrown vertically upward and it returns back. Which of the f...
Text Solution
|
- All the graphs below are intended to represent the same motion. One of...
Text Solution
|