Home
Class 12
MATHS
Let C(1) and C(2) be the graphs of the f...

Let `C_(1) and C_(2)` be the graphs of the functions `y=x^(2) and y=2x,` respectively, where `0le x le 1." Let "C_(3)` be the graph of a function y=f(x), where `0lexle1, f(0)=0.` For a point P on `C_(1),` let the lines through P, parallel to the axes, meet `C_(2) and C_(3)` at Q and R, respectively (see figure). If for every position of `P(on C_(1)),` the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

Text Solution

Verified by Experts

The correct Answer is:
`f(x)=x^(3)-x^(2), 0 le x le 1`
Promotional Banner

Topper's Solved these Questions

  • INTEGRAL CALCULUS - 2

    VMC MODULES ENGLISH|Exercise JEE Main (Archive)|64 Videos

  • FUNCTIONS

    VMC MODULES ENGLISH|Exercise JEE Main & Advanced|8 Videos

  • INTEGRAL CALCULUS-1

    VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE)|25 Videos

Similar Questions

Explore conceptually related problems

Let C_1C_2 be the graphs of the functions y=x^2 and y=2x , respectively, where 0lt=xlt=1. Let C_3 be the graph of a function y=f(x), where 0lt=xlt=1, f(0) =0. For a point P on C_1, let the lines through P , parallel to the axis, meet C_2 and C_3 at Q and R , respectively (see Figure). If for every position of P(onC_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)

Let C be the centroid of the triangle with vertices (3, -1) (1, 3) and ( 2, 4). Let P be the point of intersection of the lines x+3y-1=0 and 3x-y+1=0 . Then the line passing through the points C and P also passes through the point :

Let f(x)=" max "{x^(2),(1-x)^(2),2x(1-x)} where 0le x le 1 . Determine the area of the region bounded by y=f(x) , x-axis, x = 0 and x = 1.

Two circles C_1 and C_2 intersect at two distinct points P and Q in a line passing through P meets circles C_1 and C_2 at A and B , respectively. Let Y be the midpoint of A B and Q Y meets circles C_1 and C_2 at X a n d Z respectively. Then prove that Y is the midpoint of X Z

The circle C1 : x^2 + y^2 = 3 , with center at O, intersects the parabola x^2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii 2sqrt(3) and centers Q2 and Q3, respectively.If Q_2 and Q_3 lies on the y-axis, then

Let C_1 and C_2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let P be any point on C_1 and Q be any point C_2 . Let P_1 and Q_1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P_1 lies on C_2 and Q_1 lies on C_1 and PQ >= [P P_1, Q Q_1] . Hence or otherwise , determine points P_0 and Q_0 on the parabolas C_1 and C_2 respectively such that P_0 Q_0 <= PQ for all pairs of points (P,Q) with P on C_1 and Q on C_2

Let C_1 and C_2 be respectively, the parabolas x^2=y-1 and y^2=x-1 Let P be any point on C_1 and Q be any point on C_2 . Let P_1 and Q_1 be the refelections of P and Q, respectively with respect to the line y=x. If the point p(pi,pi^2+1) and Q(mu^2+1,mu) then P_1 and Q_1 are

Let C_1 and C_2 be respectively, the parabolas x^2=y-1 and y^2=x-1 Let P be any point on C_1 and Q be any point on C_2 . Let P_1 and Q_1 be the refelections of P and Q, respectively with respect to the line y=x. Arithemetic mean of PP_1 and Q Q_1 is always less than

Let C be a circle with centre P_(0) and AB be a diameter of C . suppose P_(1) is the midpoint of line segment P_(0) B, P_(2) the midpoint of line segment P_(1) B and so on Let C_(1),C_(2) ,C_(3) be circles with diameters P_(0)P_(1), P_(1)P_(2),P_(2)P_(3) ,... respectively Suppose the circles C_(1),C_(2),C_(2), ... are all shaded The ratio of the area of the unshaded portion of C to that of the original circle is

The graph of f(x)=x^2 and g(x)=cx^3 intersect at two points, If the area of the region over the interval [0,1/c] is equal to 2/3 , then the value of (1/c+1/(c^2)) is

VMC MODULES ENGLISH-INTEGRAL CALCULUS - 2 -JEE Advanced (Archive)
  1. Find the area of the region bounded by the curves y=x^2,y=|2-x^2|,a n ...

    Text Solution

    |

  2. Let f(x) be continuous function given by f(x)={2x ,|x|lt=1and x^2+a x+...

    Text Solution

    |

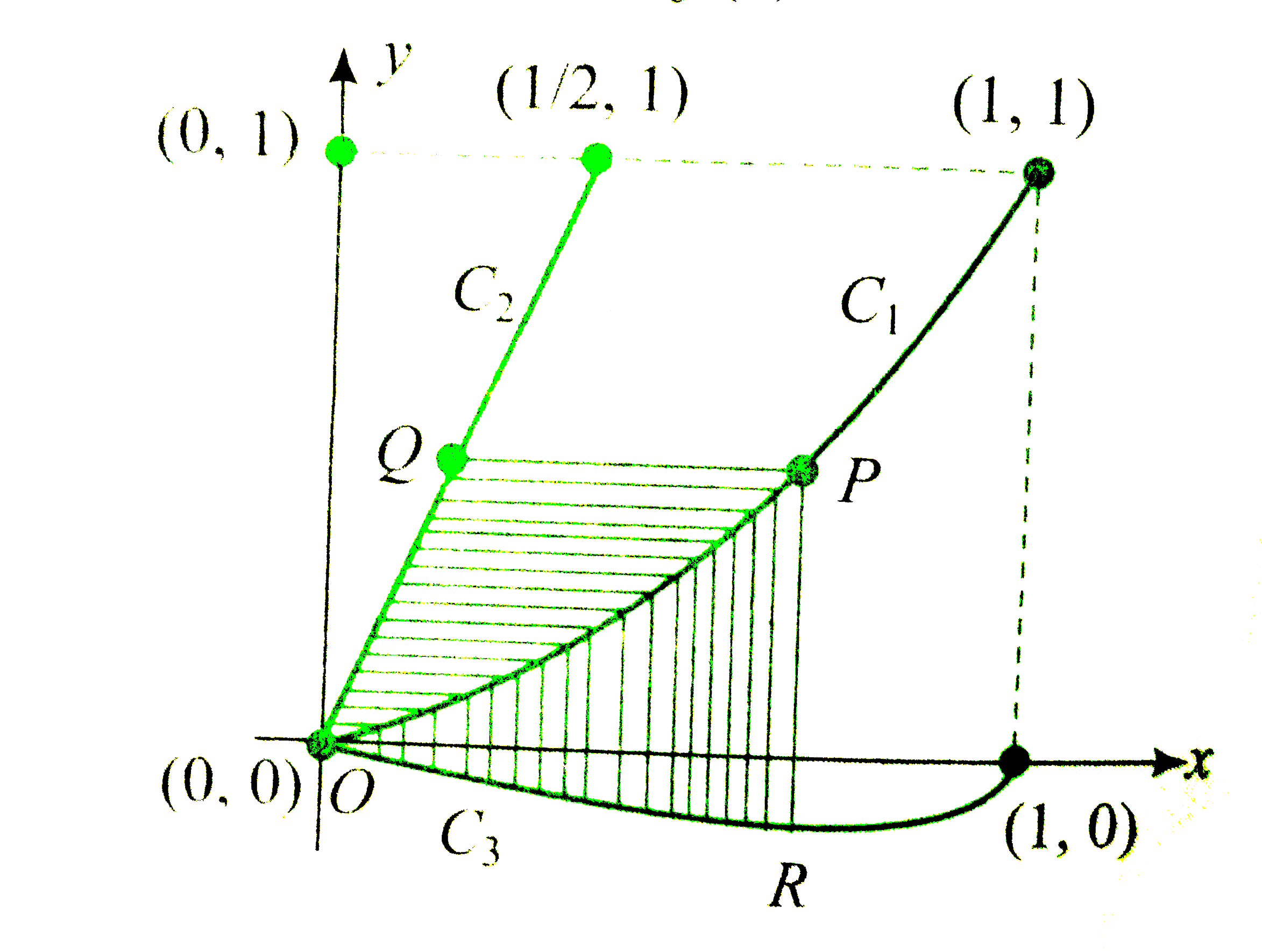
  3. Let C(1) and C(2) be the graphs of the functions y=x^(2) and y=2x, res...

    Text Solution

    |

  4. Let f(x)=M a xi mu m{x^2,(1-x)^2,2x(1-x)}, where 0lt=xlt=1. Determine ...

    Text Solution

    |

  5. Find all the possible values of b >0, so that the area of the bounded ...

    Text Solution

    |

  6. If An be the area bounded by the curve y=(tanx)^n and the lines x=0,\ ...

    Text Solution

    |

  7. In what ratio does the x-axis divide the area of the region bounded by...

    Text Solution

    |

  8. Sketch the curves and identify the region bounded by the curves x=1...

    Text Solution

    |

  9. Compute the area of the region bounded by the curves y-e x(log)e xa n ...

    Text Solution

    |

  10. Find all maxima and minima of the function y = x(x-1)^2 for 0<=x<=2 ...

    Text Solution

    |

  11. Find the area of the region bounded by the curve C: y = tan x, tangent...

    Text Solution

    |

  12. Find the area bounded by the curves x^2+y^2=25 ,4y=|4-x^2|, and x=0 ab...

    Text Solution

    |

  13. Find the area bounded by the curves x^2+y^2=4,x^2=sqrt(2)y ,a n dx=ydo...

    Text Solution

    |

  14. Sketch the region bounded by the curves y=sqrt(5-x^2) and y=|x-1| and ...

    Text Solution

    |

  15. Find the area of the region bounded by the x-axis and the curves de...

    Text Solution

    |

  16. Find the area bounded by the x-axis, part of the curve y=(1-8/(x^2)) ,...

    Text Solution

    |

  17. Find the area bounded by the curves y=2x-x^2 and the straight line y=-...

    Text Solution

    |

  18. The area of the region {(x,y): xy le 8,1 le y le x^(2)} is :

    Text Solution

    |

  19. If I=(2)/(pi)int(-pi//4)^(pi//4)(dx)/((1+e^(sin x))(2-cos 2 x)) then 2...

    Text Solution

    |

  20. The value of the integral int(0)^(pi//2)(3sqrt(costheta))/((sqrt(cos...

    Text Solution

    |