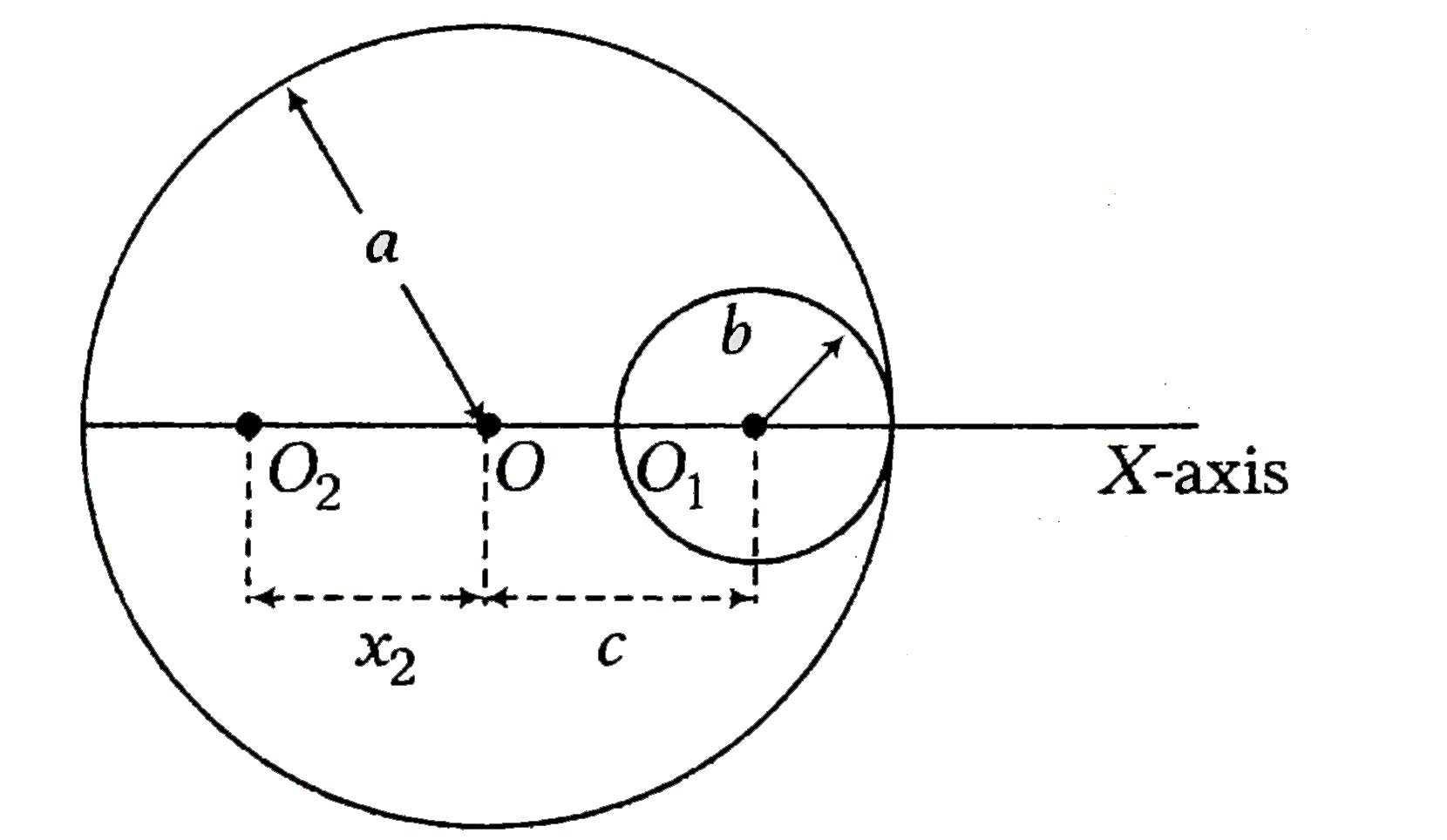
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOCK TEST 8-PHYSICS (SECTION 2)
- A uniform circular disc of radius a is taken. A circular portion of ra...
Text Solution
|
- At t=0, a particle at (1,0,0) moves towards point (4,4,12) with a cons...
Text Solution
|
- A ball impinges directly on another ball at rest. The first ball is br...
Text Solution
|
- In a Wheatstone bridge, three resistance, P, Q and R are connected in ...
Text Solution
|
- A plano convex lens fits exactly into a plano concave lens. Their plan...
Text Solution
|
- A vibrating tuning fork of frequency n is placed near the open end of ...
Text Solution
|