A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-MOCK TEST 10-MATHEMATICS (SECTION 2)
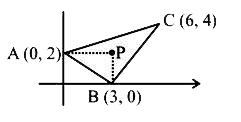
- Let A (0,2 ) , B ( 3, 0 ) , C ( 6, 4 ) be the vertices of triangle ...
Text Solution
|
- If x^(2)+y^(2)+siny=4 then the value of |(d^(2)y)/(dx^(2))| at point (...
Text Solution
|
- int((x-4)^2)/x^3dx=?
Text Solution
|
- The sum of first 50 term of the series 1+3/2+7/4+15/8+31/16+….. Is (p...
Text Solution
|
- If the variance of the first n natural numbers is 10 and t...
Text Solution
|
- Let f (x ) = | 3 - | 2- | x- 1 |||, AA x in R be not diffe...
Text Solution
|