Home
Class 12
MATHS
Find the area of the region bounded by ...

Find the area of the region bounded by `y^2=9x ,``x = 2, x = 4`and the x-axis in the first quadrant.

Text Solution

Verified by Experts

Given curve `y^(2)=9x` is a parabola which is symmetric to X-axis.

The area of the region bounded by the curve `y^(2)=9x, x=2` and `x=4` and X-axis is shown in the figure.
` :. ` Required area
`=int_(2)^(4)|y|dx=int_(2)^(4)3sqrt(x)dx`
`=3[(x^(3//2))/((3)/(2))]_(2)^(4)=(3xx2)/(3)(4^(3//2)-2^(3//2))`
`=2(4sqrt(4)-2sqrt(2))=2(8-2sqrt(2))`
`=4(4-sqrt(2))` sq. units.
Promotional Banner

Topper's Solved these Questions

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8.2|7 Videos

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|19 Videos

  • APPLICATIONS OF INTEGRALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8 C Questions For Competitive Examinations|10 Videos

  • APPLICATIONS OF DERIVATIVES

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|24 Videos

  • Continuity and Differentiability

    NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|23 Videos

Similar Questions

Explore conceptually related problems

Find the area of the region bounded by x^2=4y , y = 2, y = 4 and the y-axis in the first quadrant.

Find the area of the region bounded by x^2=4y , y = 2, y = 4 and the y-axis in the first quadrant.

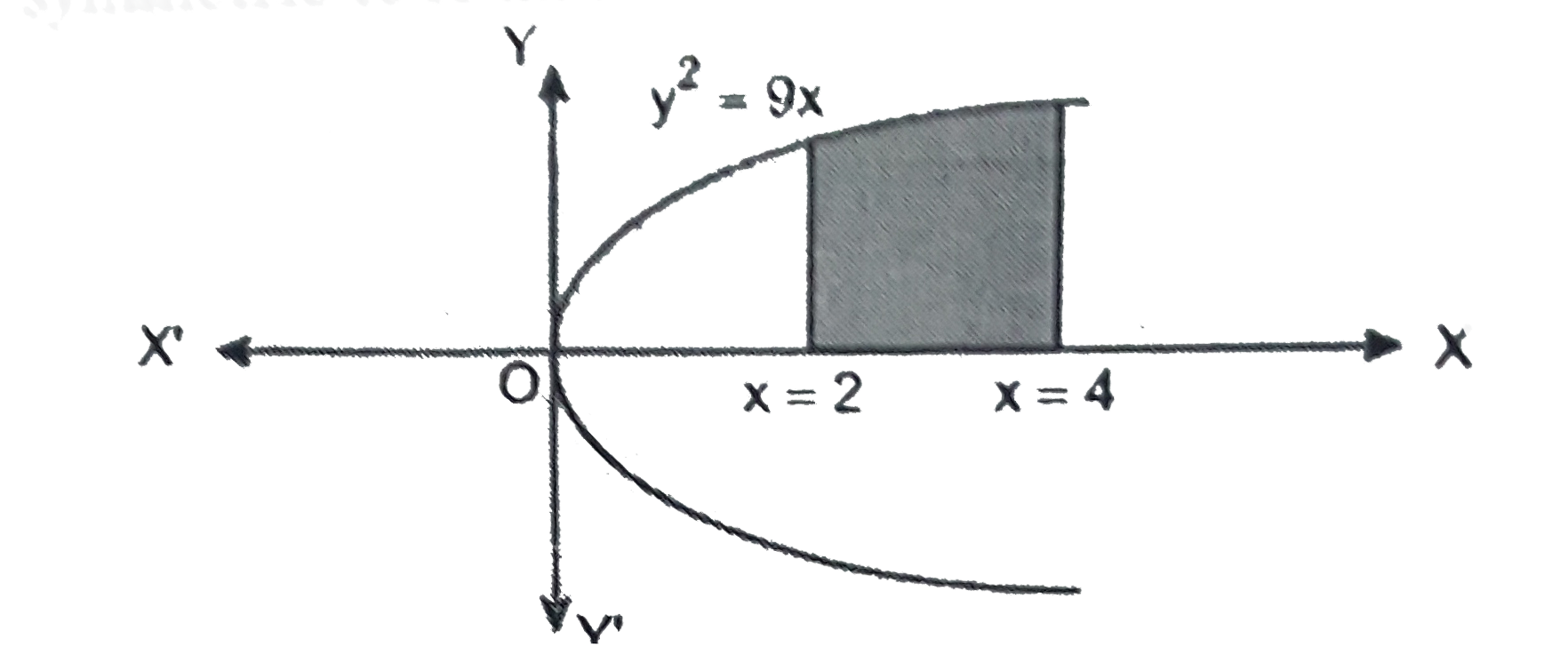
Find the area of the region bounded by y^2=4x, x=1, x=4 and the x-axis in the first quadrant.

Find the area of the region bounded by x^2=16 y ,\ y=1,\ y=4 and the y-axis in the first quadrant.

Find the area of the region bouonded by y^2=4x, x=1, x=4 and x-axis in the first quadrant.

Find the area of the region bounded by y =x^(2)+1 ,y=x ,x=0 and y=2

Find the area of the region bounded by x^(2)=8y , x-axis and the line x= 4

The area of the region bounded by the curves y=|x-2|,x=1,x=3 and the x-axis is

The area of the region bounded by the curuse y=|x-2|,x=1,x=3 and the x-axis is

Find the area of the region bounded by y=cos x and the x axis in the interval [0,2pi]