Home
Class 12
MATHS
Show that [(ptoq)^^(qto r)] to ( p to r)...

Show that `[(ptoq)^^(qto r)] to ( p to r)`is a tautology

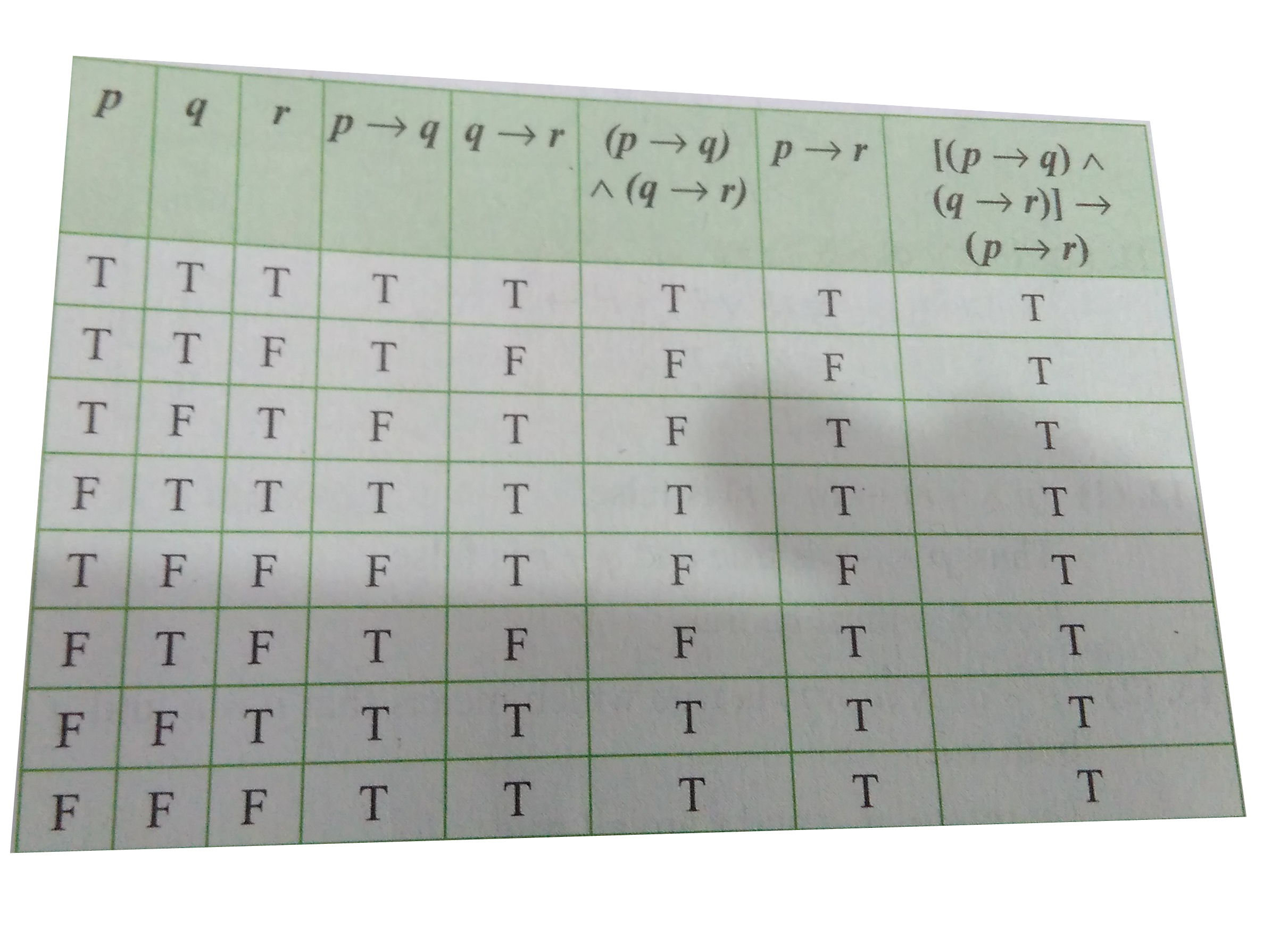
Text Solution

Verified by Experts

Truth values of `[(p to q) ^^(q to r)] to (p to r) `

For all possible truth values of p and q , the compound statement `[(p to q)^^(q to r)] to (p to r) ` is true.
Thus, `[(p to q) ^^(q to r) ] to ( p to r)` is a tautolgy.
Promotional Banner

Topper's Solved these Questions

  • MATHMETICAL REASONING

    CENGAGE|Exercise Exercise (Single)|38 Videos

  • MATHMETICAL REASONING

    CENGAGE|Exercise JEE Previous Year|10 Videos

  • MATHMETICAL REASONING

    CENGAGE|Exercise Exercise 10.1|8 Videos

  • LOGARITHM AND ITS PROPERTIES

    CENGAGE|Exercise JEE Previous Year|5 Videos

  • MATRICES

    CENGAGE|Exercise Multiple Correct Answer|7 Videos

Similar Questions

Explore conceptually related problems

Show that (p ^^ not q) vv ( not p vv q) is a tautology.

Show that ( p ^^ q) to (p vv q) is a tautology.

Show that (pvvq) to r -= (p to r) ^^ (q to r)

Show that [(pvvq)vvr] harr [pvv(qvvr)] is a tautology

Show that p vee (~p) is a tautology.

Show that (i) p to (pvvq) is a tautology (ii) (pvvq) ^^(~ p ^^~q) is a contradiction

Consider : Statement I: (p^^~q)^^(~p^^q) is a fallacy Statement II: (ptoq)harr(~q to ~p) is a tautology

Show that [ not p vv not q] vv p is a tautology.

If p^(th), q^(th), r^(th) and s^(th) terms of an A.P. are in G.P, then show that (p – q), (q – r), (r – s) are also in G.P.