
प्रश्न में दी गई संघट्ट की स्थिति को निम्न प्रकार दर्शाया जा सकता है
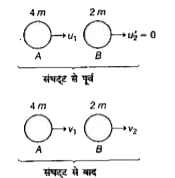
संवेग संरक्षण के सिद्धांत द्वारा,
निकाय का प्रारम्भिक संवेग= निकाय का अंतिम संवेग
`rArr (4m)u_1+ (2m)u_2. = (4m)v_1 +(2m)v_2`
` 2m(2u_1+u_2) =2m (2v_1+v_2)`
`2u_1 +u_2=2v_1+v_2`
` 2u_1 =2v_1 +v_2 " " (because v_2= 0 )...(i)`
संघट्ट से पूर्व गतिज ऊर्जा
` KE = (1)/(2) (4m) u_1^(2) +(1)/(2) (2m)u_2^(2)`
` (KE)_A = 2mu_1^(2) " " (because = u_2=0 ) `
संघट्ट के बाद गतिज ऊर्जा
`KE .= (1)/(2) (4m)v_1^(2) + (1)/(2) (2m) v_2^(2) = (2m)v_1^(2) +mv_2^(2) `
संघट्ट के पूर्व निकाय की गतिज ऊर्जा = संघट्ट के बाद निकाय की गतिज ऊर्जा
` 2mu_1^(2) = 2mv_1^(2) + mv_2^(2)`
और ` " " 2u_1^(2) = 2v_1^(2) v_2^(2) " " ...(ii)`
समी (i ) व् (ii ) को हल करने पर,
` v_1= (1)/(3) u_1` व् ` v_2= (4)/(3) u_2`
या संघट्ट के बाद A के अंतिम वेग को सूत्र द्वारा भी ज्ञात कर सकते है ,
संघट्ट के बाद निकाय का वेग
सूत्र ` " " v_1= ((m_1-m_2)/(m_1+ m_2)) u_1 + (2m_2v_2)/(m_1+m_2)`
` = ((4m-2m)/(4m+2m)) u + ( 2(2m)xx 0)/((4m+2m)) [because u_2=0]`
` = (2m)/(6m) u_1 = (1)/(3) u_1`
` therefore ` A की गतिज ऊर्जा में कुल कमी ,
` Delta KE = KE_A - KE_A. `
` " " = 2m u_1^(2) - 2mv_1^(2) = 2m(u_1^(2) -v_1^(2))`
`v_1` का मान रखने पर,
` " " Delta KE = 2m(u_1^(2) - (u_1^(2))/(9)) = (16m u _1^(2))`
` therefore ` गतिज ऊर्जा में कमी का भिनात्मक मान,
` " " (Delta KE)/(K_EA)= (16 m u_1^(2))/(9) xx (1)/(2m u_1^(2)) = (8)/(9)`