त्रिज्या R के किसी बेलनाकार चालक से कोई नियत धारा प्रवाहित हो रही है। चुम्बकीय क्षेत्र, B के परिमाण तथा चालक के केंद्र से दुरी , d के बीच ग्राफ का सही निरोपण निम्नलिखित में से किस आरेख द्वारा किया गया है?

Options

A.
B.
C.
D.

Answer

C

Explanation

माना बेलन R त्रिज्या के संकेन्द्रिव वृतों से मिलकर बना है।

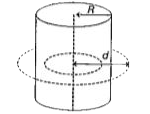
(i) बेलन के बाह्य बिंदु पर चुंबकीय क्षेत्र ` d gt R `
एम्पियर के परिपथीय नियम द्वारा ` oint B. dl = mu_0 I`
` rArr " " B int dl = mu_0 I`
` " " B ( 2pi d) = mu_0 I`
` rArr " " B= ( mu_0 I)/(2pi d) `
यहाँ `mu_0` = निर्वात की चुंबकशीलता (ii ) सतह पर चुंबकीय क्षेत्र , d = R
` " " B = (mu_0I)/(2pi R ) `
(iii) आंतरिक बिंदु पर चुंबकीय क्षेत्र बेलन के अंदर स्थित बिंदु के लिए धारा , I . = बेलन के एकांक अनुप्रस्थ काट की धारा `xx ` लूप का अनुप्रस्थ - काट क्षेत्रफल
` " " (I)/(pi R^(2)) pi d^(2) = (Id^(2))/(R^(2))`
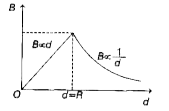
` therefore " " B = ( mu_0I)/(2pi d) = ( mu_0Id^(2))/( 2pi R^(2) d) = ( mu_0I)/(2pi R^(2)) d `
चुंबकीय क्षेत्र में परिवर्तन का ग्राफ निम्न होगा