A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Linked|10 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Matrix match type|4 VideosCOORDINATE SYSYEM
CENGAGE PUBLICATION|Exercise Exercises|59 VideosCOORDINATE SYSTEM
CENGAGE PUBLICATION|Exercise Multiple Correct Answers Type|2 VideosCROSS PRODUCTS
CENGAGE PUBLICATION|Exercise DPP 2.2|13 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-COORDINATE SYSYEM -Multiple correct
- If (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then rem...
Text Solution
|
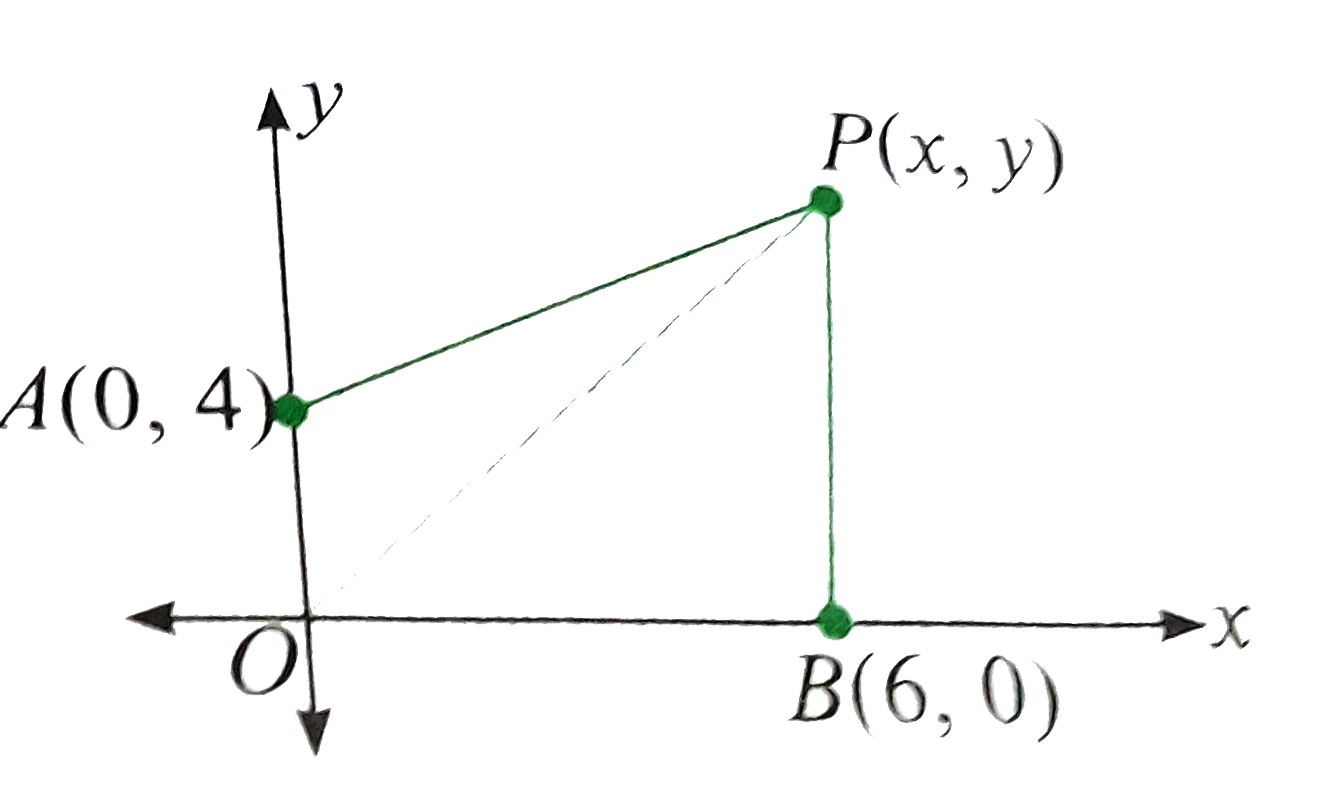
- Let 0-=(0,0),A-=(0,4),B-=(6,0)dot Let P be a moving point such that th...
Text Solution
|
- If (-4,0) and (1,-1) are two vertices of a triangle of area 4s qdotu n...
Text Solution
|
- The area of triangle A B C is 20c m^2dot The coordinates of vertex A a...
Text Solution
|
- If A B C having vertices A(acostheta1,asintheta1),B(acostheta2asin...
Text Solution
|
- The points A(0,0),B(cosalpha,sinalpha) and C(cosbeta,sinbeta) are the ...
Text Solution
|
- The ends of a diagonal of a square are (2,-3) and (-1,1)dot Another ve...
Text Solution
|
- If all the vertices of a triangle have integral coordinates, then th...
Text Solution
|
- In a A B C ,A-=(alpha,beta),B-=(1,2),C-=(2,3), point A lies on the li...
Text Solution
|
- In an acute triangle A B C , if the coordinates of orthocentre H are (...
Text Solution
|
- Consider the points O(0,0), A(0,1), and B(1,1) in the x-y plane. Suppo...
Text Solution
|
- Two sides of a rhombus ABCD are parallel to the lines y=x+2 and y=7x+3...
Text Solution
|
- A right angled triangle ABC having a right angle at C, CA=b and CB=a, ...
Text Solution
|